Câu hỏi:
20/06/2024 363Cho hình nón \((N)\) có góc ở đỉnh bằng \(120^\circ .\) Mặt phẳng qua trục của \((N)\), cắt \((N)\) theo một thiết diện là tam giác có bán kính đường tròn ngoại tiếp bằng 4. Thể tích của khối nón \((N)\) là
Quảng cáo
Trả lời:
Giải bởi Vietjack
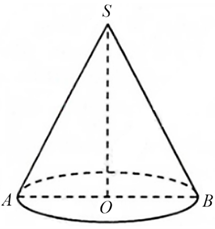
Gọi tam giác \[SAB\] là thiết diện của hình nón khi cắt bởi mặt phẳng đi qua đỉnh.
Và \(R\) là bán kính đường tròn ngoại tiếp tam giác \[SAB,{\rm{ }}r\] là bán kính hình nón.
Áp dụng định lý sin trong tam giác \[SAB\], ta có:
\(\frac{{AB}}{{\sin \widehat {ASB}}} = 2R \Rightarrow AB = 2R \cdot \sin \widehat {ASB} = 4\sqrt 3 \Rightarrow r = \frac{{AB}}{2} = 2\sqrt 3 .\)Mặt khác, \(\tan \widehat {OSB} = \frac{{OB}}{{SO}} \Rightarrow SO = h = \frac{{OB}}{{\tan \widehat {OSB}}} = \frac{r}{{\tan 60^\circ }} = 2.\)
Thể tích khối nón là \(V = \frac{1}{3}\pi {r^2}h \Rightarrow V = \frac{1}{3}\pi {\left( {2\sqrt 3 } \right)^2} \cdot 2 = 8\pi .\) Chọn A.
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\) là số hành khách trên mỗi chuyến xe để nhà xe thu được lợi nhuận lớn nhất.
Gọi \(F\left( x \right)\) là hàm chỉ số tiền thu được sau mỗi chuyến xe \(\left( {0 < x \le 60\,,\,\,x \in \mathbb{N}} \right).\)
Số tiền thu được sau mỗi chuyến xe:
\(F\left( x \right) = {\left( {300 - \frac{{5x}}{2}} \right)^2} \cdot x = 90\,\,000x - 1500{x^2} + \frac{{25}}{4}{x^3}\).
Bài toán trở thành tìm \(x\) để \(F(x)\) đạt giá trị lớn nhất thì \(F'\left( x \right) = 90\,\,000 - 3\,\,000x + \frac{{75}}{4}{x^2}\)
\(F'\left( x \right) = 0 \Leftrightarrow 90\,\,000 - 3\,\,000x + \frac{{75}}{4}{x^2} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 120}&{(L)}\\{x = 40}&{(TM)}\end{array}.} \right.\)
Bảng biến thiên:
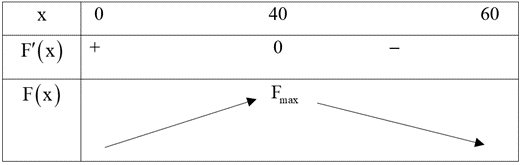
Vậy để thu được lợi nhuận của mỗi chuyến xe là lớn nhất thì mỗi chuyến xe phải chở 40 người.
Lời giải
Gọi \(H\) là hình chiếu vuông góc của \(A\left( {2\,;\,\, - 3\,;\,\,5} \right)\) lên \[Oy.\]
Suy ra \(H\left( {0\,;\,\, - 3\,;\,\,0} \right).\) Khi đó \(H\) là trung điểm đoạn \(AA'.\)
Do đó \[\left\{ {\begin{array}{*{20}{l}}{{x_H} = \frac{{{x_A} + {x_{A'}}}}{2}}\\{{y_H} = \frac{{{y_A} + {y_{A'}}}}{2}}\\{{z_H} = \frac{{{z_A} + {z_{A'}}}}{2}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_{A'}} = 2{x_H} - {x_A} = 2 \cdot 0 - 2 = - 2}\\{{y_{A'}} = 2{y_H} - {y_A} = 2 \cdot \left( { - 3} \right) - ( - 3) = - 3}\\{{z_{A'}} = 2{z_H} - {z_A} = 2 \cdot 0 - 5 = - 5}\end{array}} \right.} \right.\].
\[ \Rightarrow A'\left( { - 2\,;\,\, - 3\,;\,\, - 5} \right).\] Chọn D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 30)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 3)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận