Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 8)
77 người thi tuần này 4.6 2.7 K lượt thi 150 câu hỏi 150 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 45)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 44)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 43)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 42)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 41)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 40)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 39)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 38)
Danh sách câu hỏi:
Lời giải
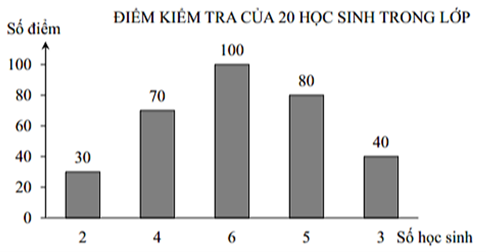
Dựa vào biểu đồ trên, điểm trung bình (trung bình số học) trong bài kiểm tra là:
\(\frac{{30 \cdot 2 + 70 \cdot 4 + 100 \cdot 6 + 80 \cdot 5 + 40 \cdot 3}}{{2 + 4 + 6 + 5 + 3}} = 73\) (điểm).
Vậy điểm trung bình (trung bình số học) trong bài kiểm tra là 73 điểm.
Chọn B.
Lời giải
Có: \(f\left( x \right) = \frac{1}{5}{x^5} - {x^3} + 7x - 3 \Rightarrow f'\left( x \right) = {x^4} - 3{x^2} + 7.\)
Thay (1) vào bất phương trình: \(f'\left( x \right) - 11 \le 0\)\( \Rightarrow {x^4} - 3{x^2} - 4 \le 0\)
\( \Leftrightarrow \left( {{x^2} + 1} \right)\left( {{x^2} - 4} \right) \le 0 \Leftrightarrow \left( {x - 2} \right)\left( {x + 2} \right) \le 0 \Leftrightarrow - 2 \le x \le 2.\)
Vậy số nghiệm nguyên của bất phương trình là 5.
Chọn A.
Lời giải
Điều kiện: \(x > 3.\)
Ta có \({\log _2}\left( {x - 3} \right) + 2{\log _4}3 \cdot {\log _3}x = 2\)\( \Leftrightarrow {\log _2}\left( {x - 3} \right) + 2{\log _4}x = 2\)
\( \Leftrightarrow {\log _2}\left( {x - 3} \right) + 2{\log _{{2^2}}}x = 2\)\( \Leftrightarrow {\log _2}\left( {x - 3} \right) + {\log _2}x = 2\)
\( \Leftrightarrow {\log _2}\left( {x - 3} \right)x = 2 \Leftrightarrow x(x - 3) = 4\)\( \Leftrightarrow {x^2} - 3x - 4 = 0 \Rightarrow \left[ {\begin{array}{*{20}{l}}{x = 4}\\{x = - 1\,\,(L)}\end{array}} \right.\).
Vậy phương trình đã cho có nghiệm duy nhất. Chọn A.
Lời giải
Ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{{x^2} + xy + {y^2} = 3}&{{\rm{ (1) }}}\\{{x^3} + 3\left( {y - x} \right) = 1}&{{\rm{ (2) }}}\end{array}} \right.\)
Thay \(3 = {x^2} + xy + {y^2}\) vào (2) ta được:
\({x^3} + \left( {{x^2} + xy + {y^2}} \right)\left( {y - x} \right) = 1 \Leftrightarrow {x^3} + \left( {{y^3} - {x^3}} \right) = 1 \Leftrightarrow {y^3} = 1 \Leftrightarrow y = 1.\)
Thay \(y = 1\) vào (1) ta được: \({x^2} + x - 2 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 2}\\{x = 1}\end{array}} \right..\)
Vậy hệ phương trình có 2 nghiệm. Chọn B.
Câu 5
Lời giải
Ta có \[G\] là trọng tâm tam giác \[ABC\] nên
\(\left\{ {\begin{array}{*{20}{l}}{{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}}\\{{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_G} = \frac{{ - 4 + 1 + 6}}{3} = - 3}\\{{y_G} = \frac{{1 + 3 + 0}}{3} = \frac{4}{3}}\end{array}} \right.} \right.\)\( \Rightarrow G\left( { - 3\,;\,\,\frac{4}{3}} \right) \Rightarrow {z_G} = - 3 + \frac{4}{3}i\). Chọn A.
Câu 6
A. \(3x - 2y + z - 4 = 0.\)
B. \(3x - 2y + z + 4 = 0.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A. \[144\,\,980\,\,000\] đồng.
B. \[103\,\,144\,\,000\] đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
A. \[21\,\,800\,\,000\] đồng.
B. \[20\,\,800\,\,000\] đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 27
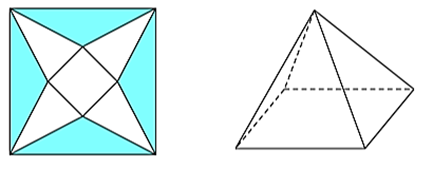
A. \(711,6\;\,{\rm{c}}{{\rm{m}}^3}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 28
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 29
A. \(\frac{{x - 1}}{2} = \frac{y}{{ - 2}} = \frac{{z - 2}}{1}.\)
B. \(\frac{{x - 1}}{4} = \frac{y}{{ - 1}} = \frac{{z - 2}}{1}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 33
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 34
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 35
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 51
A. ích kỉ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 52
A. tiêu cực.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 53
A. những.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 54
A. nghệ thuật.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 55
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 56
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 57
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 58
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 59
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 60
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 61
A. phát tán.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 62
A. Văn học hiện thực.
B. Truyện ngắn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 63
A. Phục vụ cách mạng.
B. Hướng về đại chúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 64
A. thi vị hóa.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 65
A. theo – mà còn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 67
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 70
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 72
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 73
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 74
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 75
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 77
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 78
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 79
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 80
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 81
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 82
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 83
Nhờ được viện trợ kinh tế của Mĩ qua Kế hoạch Mácsan, bước sang năm 1950 nền kinh tế các nước Tây Âu
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 84
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 85
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 86
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 87
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 88
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 89
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 90
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 92
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 93
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 94
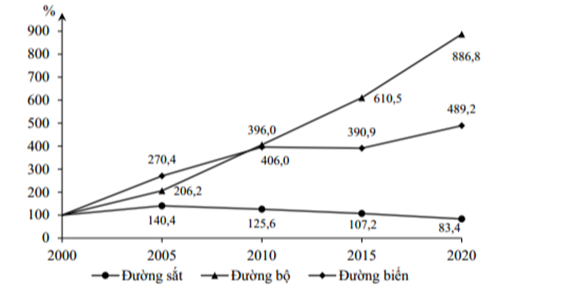
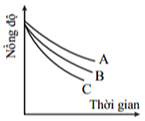
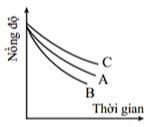
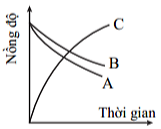
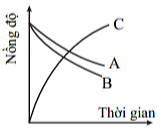
A. Tốc độ tăng trưởng khối lượng hàng hóa vận chuyển bắng đường sắt nước ta giai đoạn 2000-2020.
B. Tốc độ tăng trưởng khối lượng hàng hóa vận chuyển một số ngành vận tải nước ta giai đoạn 2000 -2020.
C. Tốc độ tăng trưởng khối lượng hàng hóa luân chuyển một số ngành vận tải nước ta giai đoạn 2000 -2020.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 95
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 96
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 97
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 98
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 99
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 100
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 101
A. Khúc xạ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 103
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 104
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 105
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 106
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 108
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 109
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 110
A. \(1,25{\rm{M}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 111
A. 18,71.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 112
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 113
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 114
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 115
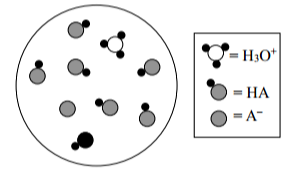
Cho sơ đồ sự phân li của \({\rm{NaCl}}\) trong môi trường \({{\rm{H}}_2}{\rm{O}}\):
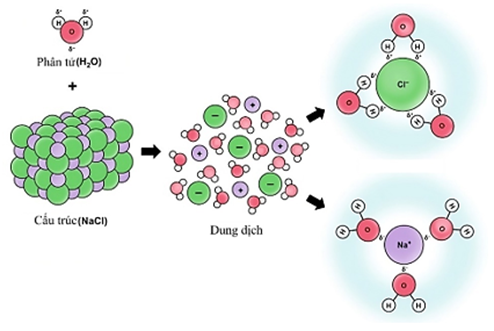
Cho các phát biểu:
(a) Các phân tử \({{\rm{H}}_2}{\rm{O}}\) có tương tác với các ion.
(b) \({{\rm{H}}_2}{\rm{O}}\) là một chất phân cực, nguyên tử \({\rm{H}}\) mang một phần điện tích âm, nguyên tử O mang một phần điện tích dương.
(c) Các phân tử \({{\rm{H}}_2}{\rm{O}}\) sẽ kéo ion ra khỏi cấu trúc tinh thể \({\rm{NaCl}}\).
(d) Các phân tử \({{\rm{H}}_2}{\rm{O}}\) sẽ bao quanh các ion \({\rm{N}}{{\rm{a}}^ + }\)và \({\rm{C}}{{\rm{l}}^ - }.\)
Trong các phát biểu trên, số phát biểu đúng là
Cho sơ đồ sự phân li của \({\rm{NaCl}}\) trong môi trường \({{\rm{H}}_2}{\rm{O}}\):

Cho các phát biểu:
(a) Các phân tử \({{\rm{H}}_2}{\rm{O}}\) có tương tác với các ion.
(b) \({{\rm{H}}_2}{\rm{O}}\) là một chất phân cực, nguyên tử \({\rm{H}}\) mang một phần điện tích âm, nguyên tử O mang một phần điện tích dương.
(c) Các phân tử \({{\rm{H}}_2}{\rm{O}}\) sẽ kéo ion ra khỏi cấu trúc tinh thể \({\rm{NaCl}}\).
(d) Các phân tử \({{\rm{H}}_2}{\rm{O}}\) sẽ bao quanh các ion \({\rm{N}}{{\rm{a}}^ + }\)và \({\rm{C}}{{\rm{l}}^ - }.\)
Trong các phát biểu trên, số phát biểu đúng là
A. 1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 119
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 120
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 121
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 122
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 123
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 125
A. loại bỏ kiểu gen đồng hợp trội và kiểu gen đồng hợp lặn.
B. loại bỏ kiểu gen đồng hợp lặn và kiểu gen dị hợp.
C. loại bỏ kiểu gen dị hợp và giữ lại các kiểu gen đồng hợp.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 1
Đọc đoạn trích sau và trả lời các câu hỏi từ 51 đến 55:
Nếu bước chân vào bất kì bệnh viện nào và hỏi bác sĩ về “bệnh vô cảm”, chắc chắn bạn sẽ không nhận được câu trả lời. Bởi đó là căn bệnh tồn tại ngoài xã hội chứ không phải đơn thuần trên giường bệnh. “Bệnh vô cảm” là tình trạng chai sạn của tâm hồn, là thái độ sống thờ ơ, lãnh đạm trước những gì diễn ra xung quanh mình. Đáng sợ hơn là nó diễn ra ngay cả trước những đau khổ, mất mát của con người. Một ngày, bạn không còn biết yêu thương và cũng không căm ghét, không cảm nhận được hạnh phúc và cũng không động lòng trước đau khổ, không có khát vọng sống ý nghĩa... thì ắt hẳn, bạn đang có những “triệu chứng” của căn bệnh vô cảm đáng sợ kia. Nó không làm con người ta đau đớn hay chết đi về thể xác nhưng lại làm trái tim và tâm hồn chết dần trong sự lạnh lẽo. Và phải chăng “cái chết không phải là điều mất mát lớn nhất trong cuộc đời, sự mất mát lớn nhất là bạn để tâm hồn tàn lụi ngay khi còn sống” như lời Nooc- man Ku-sin đã khẳng định?
(Theo Bài tập Ngữ văn 12, tập hai, NXB Giáo dục Việt Nam-2011)
Câu 128
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 129
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 130
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 131
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 132
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 2
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 56 đến 60:
(1) Những người vợ nhớ chồng còn góp cho Đất Nước những núi Vọng Phu
(2) Cặp vợ chồng yêu nhau góp nên hòn Trống Mái
(3) Gót ngựa của Thánh Gióng đi qua còn trăm ao đầm để lại
(4) Chín mươi chín con voi góp mình dựng đất Tổ Hùng Vương
(5) Những con rồng nằm im góp dòng sông xanh thẳm
(6) Người học trò nghèo góp cho Đất Nước mình núi Bút, non Nghiên
(7) Con cóc, con gà quê hương cùng góp cho Hạ Long thành thắng cảnh
(8) Những người dân nào đã góp tên Ông Đốc, Ông Trang, Bà Đen, Bà Điểm
(9) Và ở đâu trên khắp ruộng đồng gò bãi
(10) Chẳng mang một dáng hình, một ao ước, một lối sống ông cha
(11) Ôi Đất Nước sau bốn nghìn năm đi đâu ta cũng thấy
(12) Những cuộc đời đã hóa núi sông ta ....
(Đất Nước – Nguyễn Khoa Điềm)
Câu 133
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 134
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 135
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 136
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 137
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 61 đến 65:
Ngày nay, có quá nhiều phụ huynh chỉ biết con mình đang bị sỉ nhục, đang phải chịu đựng sự ức hiếp khi đã quá muộn. Hàng ngày, người ta online, đặc biệt là những người trẻ – những người chưa được trang bị để đối phó với điều này, và vì thế họ bị lạm dụng, bị làm tổn thương đến mức không thể tưởng tượng có thể sống tiếp tới ngày hôm sau nữa hay không, và một số thảm kịch đã xảy ra. Nó không còn ở trong thế giới ảo nữa. ChildLine – một tổ chức phi lợi nhuận của Anh chuyên giải quyết những vấn đề của người trẻ đã đưa ra một thống kê đáng kinh ngạc vào năm ngoái: từ năm 2012 tới 2013, các cuộc gọi và email yêu cầu được giúp đỡ liên quan tới xúc phạm trong thế giới ảo tăng tới 87%. Một phân tích tổng hợp cho thấy, lần đầu tiên tỉ lệ tự tử vì bị sỉ nhục trên mạng nhiều hơn đáng kể so với bị ức hiếp trực tiếp. Và điều hoảng hốt là một nghiên cứu khác vào năm ngoái chỉ ra rằng sự sỉ nhục mang lại cảm giác mạnh hơn cả hạnh phúc và tức giận.
Chế giễu công khai là một môn thể thao đổ máu cần phải dừng lại. Hãy bình luận bằng những ngôn từ tích cực, tiếp nhận tin tức và click chuột bằng sự bao dung, bởi chúng ta đã gieo những hạt giống của sự xấu hổ và sự tổn thương trên mảnh đất văn hóa của mình, cả ở thế giới thật và ảo.
(Bài thuyết trình chấn động của nữ thực tập sinh nổi tiếng – Vietnamnet.vn)
Câu 138
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 139
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 140
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 141
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 142
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 66 đến 70:
Chớ tự kiêu, tự đại. Tự kiêu, tự đại là khờ dại. Vì mình hay, còn nhiều người hay hơn mình. Mình giỏi, còn nhiều người giỏi hơn mình. Tự kiêu, tự đại tức là thoái bộ. Sông to, biển rộng, thì bao nhiêu nước cũng chứa được, vì độ lượng nó rộng và sâu. Cái chén nhỏ, cái đĩa cạn, thì một chút nước cũng đầy tràn, vì độ lượng nó hẹp nhỏ. Người mà tự kiêu, tự mãn, cũng như cái chén, cái đĩa cạn…
(Trích Cần kiệm liêm chính, Hồ Chí Minh, tháng 6-1949)
Câu 143
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 144
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 145
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 146
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 147
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 5
Dựa vào các thông tin sau đây để trả lời các câu hỏi từ câu 108 đến câu 110:
"Hiệp định Giơnevơ năm 1954 về Đông Dương Bao gồm các văn bản: Hiệp định đinh chí chiến sự ở Việt Nam, Lào, Campuchia; Bản tuyên bố cuối cùng của Hội nghị và các phụ bản khác.
Các nước tham dự Hội nghị cam kết tôn trọng các quyền dân tộc cơ bản là độc lập, chủ quyền, thống nhất và toàn vẹn lãnh thổ của Ba nước Việt Nam, Lào, Campuchia; cam kết không can thiệp vào công việc nội bộ của Ba nước.
- Các bên tham chiến thực hiện ngừng bắn, lập lại hòa bình trên toàn Đông Dương.
- Các bên tham chiến thực hiện cuộc tập kết, chuyển quân, chuyển giao khu vực.
+ Ở Việt Nam, quân đội nhân dân Việt Nam và quân đội viễn chinh Pháp tập kết ở hai miền Bắc-Nam, lấy vĩ tuyến 17 (dọc theo sông Bến Hải-Quảng Trị) làm giới tuyến quân sự tạm thời cùng với một khu phi quân sự ở hai bên giới tuyến.
+ Ở Lào, lực lượng kháng chiến tập kết ở hai tỉnh Sầm Nưa và Phongxalì.
+ Ở Campuchia, lực lượng kháng chiến phục viên tại chỗ, không có vùng tập kết.
- Hiệp định cấm đưa quân đội, nhân viên quân sự, vũ khí nước ngoài vào các nước Đông Dương. Các nước ngoài không được đặt căn cứ quân sự ở Đông Dương. Các nước Đông Dương không được tham gia bất cứ khối liên minh quân sự nào và không để cho nước khác dùng lãnh thổ của mình vào việc gây chiến tranh hoặc phục vụ cho mục đích xâm lược.
- Việt Nam tiến tới thống nhất bẳng cuộc tổng tuyển cử tự do trong cả nước sē được tổ chức vào tháng 7-1956 dưới sự kiểm soát và giám sát của một Uỷ Ban quốc tế (gồm Ấn Độ làm Chủ tịch, cùng hai thành viên là BA Lan và Canađa).
- Trách nhiệm thi hành Hiệp định Giơnevơ thuộc về những người kí Hiệp định và những người kế tục họ. Hiệp định Giơnevơ năm 1954 về Đông Dương là văn bản pháp lí quốc tế ghi nhận các quyền dân tộc cơ bản của nhân dân các nước Đông Dương và được các cường quốc cùng các nước tham dự Hội nghị cam kết tôn trọng. Nó đánh dấu thắng lợi của cuộc kháng chiến chống Pháp của nhân dân ta, song chưa trọn vẹn vì mới giải phóng được miền Bắc Cuộc đấu tranh cách mạng vẫn phải tiếp tục nhằm giải phóng miền Nam, thống nhất đất nước.
Với Hiệp định Giơnevơ năm 1954 về Đông Dương, Pháp Buộc phải chấm dứt chiến tranh xâm lược, rút hết quân đội về nước Mĩ thất bại trong âm mưu kéo dài, mở rộng, quốc tế hoá chiến tranh xâm lược Đông Dương".
(Nguồn: SGK Lịch sử 12, NXB Giáo dục Việt Nam, 2023, trang 154-155).
Câu 148
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 149
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 150
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.