Câu hỏi:
07/08/2024 123
Cho biết bệnh bạch tạng do gen lặn nằm trên nhiễm sắc thể thường quy định, bệnh mù màu do gen lặn nằm trên nhiễm sắc thể giới tính X quy định. Ở một cặp vợ chồng đều không bị hai bệnh này, bên phía người vợ có ông ngoại bị mù màu, mẹ của cô ta bị bạch tạng. Bên phía người chồng có ông nội và mẹ bị bạch tạng. Những người khác trong hai dòng họ này đều không bị hai bệnh nói trên. Cặp vợ chồng này dự định sinh hai đứa con, xác suất để cả hai đứa con của họ đều không bị hai bệnh nói trên là bao nhiêu? (làm tròn đến số thập phân thứ 3)
Đáp án: ……….
Cho biết bệnh bạch tạng do gen lặn nằm trên nhiễm sắc thể thường quy định, bệnh mù màu do gen lặn nằm trên nhiễm sắc thể giới tính X quy định. Ở một cặp vợ chồng đều không bị hai bệnh này, bên phía người vợ có ông ngoại bị mù màu, mẹ của cô ta bị bạch tạng. Bên phía người chồng có ông nội và mẹ bị bạch tạng. Những người khác trong hai dòng họ này đều không bị hai bệnh nói trên. Cặp vợ chồng này dự định sinh hai đứa con, xác suất để cả hai đứa con của họ đều không bị hai bệnh nói trên là bao nhiêu? (làm tròn đến số thập phân thứ 3)
Đáp án: ……….
Quảng cáo
Trả lời:
Giải bởi Vietjack
- Quy ước: gen A bình thường >> a bạch tạng; gen B bình thường >> b bị bệnh mù màu.
- Xét tính trạng bạch tạng:
Người vợ bình thường nhưng mẹ bị bạch tạng (aa) → Người vợ có kiểu gen là Aa.
Người chồng bình thường nhưng mẹ bị bạch tạng (aa) → Người chồng có kiểu gen là Aa.
P: Aa × Aa → Xác suất sinh 2 con không bị bệnh bạch tạng của cặp vợ chồng này là:
\(1 \times 1 \times {\left( {\frac{3}{4}} \right)^2} = \frac{9}{{16}}\)
- Xét tính trạng mù màu:
Ông ngoại của người vợ bị mù màu (XbY) → Mẹ của người vợ có kiểu hình bình thường sẽ có kiểu gen là \({X^B}{X^b}\), bố của người vợ bình thường có kiểu gen là \({X^B}Y\) → Người vợ có xác suất về kiểu gen là: \(\left( {\frac{1}{2}{X^B}{X^B}:\frac{1}{2}{X^B}{X^b}} \right)\).
Người chồng bình thường có kiểu gen là\({X^B}Y\).
P: \(\left( {\frac{1}{2}{X^B}{X^B}:\frac{1}{2}{X^B}{X^b}} \right)\)×\({X^B}Y\)
TH1: Nếu người vợ có kiểu gen là \({X^B}{X^B}\) thì xác suất sinh 2 con không bị bệnh mù màu là:
\(\frac{1}{2} \times 1 \times {1^2} = \frac{1}{2}\)
TH2: Nếu người vợ có kiểu gen là \({X^B}{X^b}\) thì xác suất sinh 2 con không bị bệnh mù màu là:
\(\frac{1}{2} \times 1 \times {\left( {1 - \frac{1}{4}} \right)^2} = \frac{9}{{32}}\)
→ Xác suất sinh 2 con không bị bệnh mù màu của cặp vợ chồng này là: \(\frac{1}{2} + \frac{9}{{32}} = \frac{{25}}{{32}}\)
Vậy xác suất để cặp vợ chồng này sinh 2 đứa con không bị cả 2 bệnh là:
\(\frac{9}{{16}} \times \frac{{25}}{{32}} = \frac{{225}}{{512}} = 0,439.\)
Đáp án: 0,439
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\) là số hành khách trên mỗi chuyến xe để nhà xe thu được lợi nhuận lớn nhất.
Gọi \(F\left( x \right)\) là hàm chỉ số tiền thu được sau mỗi chuyến xe \(\left( {0 < x \le 60\,,\,\,x \in \mathbb{N}} \right).\)
Số tiền thu được sau mỗi chuyến xe:
\(F\left( x \right) = {\left( {300 - \frac{{5x}}{2}} \right)^2} \cdot x = 90\,\,000x - 1500{x^2} + \frac{{25}}{4}{x^3}\).
Bài toán trở thành tìm \(x\) để \(F(x)\) đạt giá trị lớn nhất thì \(F'\left( x \right) = 90\,\,000 - 3\,\,000x + \frac{{75}}{4}{x^2}\)
\(F'\left( x \right) = 0 \Leftrightarrow 90\,\,000 - 3\,\,000x + \frac{{75}}{4}{x^2} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 120}&{(L)}\\{x = 40}&{(TM)}\end{array}.} \right.\)
Bảng biến thiên:
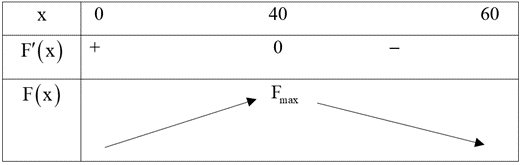
Vậy để thu được lợi nhuận của mỗi chuyến xe là lớn nhất thì mỗi chuyến xe phải chở 40 người.
Lời giải
Gọi \(H\) là hình chiếu vuông góc của \(A\left( {2\,;\,\, - 3\,;\,\,5} \right)\) lên \[Oy.\]
Suy ra \(H\left( {0\,;\,\, - 3\,;\,\,0} \right).\) Khi đó \(H\) là trung điểm đoạn \(AA'.\)
Do đó \[\left\{ {\begin{array}{*{20}{l}}{{x_H} = \frac{{{x_A} + {x_{A'}}}}{2}}\\{{y_H} = \frac{{{y_A} + {y_{A'}}}}{2}}\\{{z_H} = \frac{{{z_A} + {z_{A'}}}}{2}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_{A'}} = 2{x_H} - {x_A} = 2 \cdot 0 - 2 = - 2}\\{{y_{A'}} = 2{y_H} - {y_A} = 2 \cdot \left( { - 3} \right) - ( - 3) = - 3}\\{{z_{A'}} = 2{z_H} - {z_A} = 2 \cdot 0 - 5 = - 5}\end{array}} \right.} \right.\].
\[ \Rightarrow A'\left( { - 2\,;\,\, - 3\,;\,\, - 5} \right).\] Chọn D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 30)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 3)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận