Cho hàm số \(f\left( x \right)\) có đạo hàm xác định trên \(\mathbb{R}.\) Biết \(f\left( 1 \right) = 2\) và \(\int\limits_0^1 {{x^2}f'\left( x \right){\rm{d}}x} = \int\limits_1^4 {\frac{{1 + 3\sqrt x }}{{2\sqrt x }}f\left( {2 - \sqrt x } \right){\rm{d}}x} = 4.\) Giá trị của \(\int\limits_0^1 {f\left( x \right){\rm{d}}x} \) bằng
Quảng cáo
Trả lời:
Đặt \(t = 2 - \sqrt x \Leftrightarrow {\rm{d}}t = - \frac{1}{{2\sqrt x }}\;{\rm{d}}x \Leftrightarrow - {\rm{d}}t = \frac{1}{{2\sqrt x }}\;{\rm{d}}x\)
Đổi cận: \(x = 1 \Rightarrow t = 1\,;\,\,x = 4 \Rightarrow t = 0.\)
Do đó \(\int\limits_1^4 {\frac{{1 + 3\sqrt x }}{{2\sqrt x }}f\left( {2 - \sqrt x } \right){\rm{d}}x} = 4 \Leftrightarrow \int\limits_1^4 {\left( {1 + 3\sqrt x } \right)f\left( {2 - \sqrt x } \right)\frac{{{\rm{d}}x}}{{2\sqrt x }} = 4} \)
\( \Leftrightarrow \int\limits_1^0 {\left( {7 - 3t} \right)f\left( t \right)\left( { - {\rm{d}}t} \right)} = 4 \Leftrightarrow \int\limits_0^1 {\left( {7 - 3x} \right)f\left( x \right){\rm{d}}x} = 4.\)
Ta có \(\int\limits_0^1 {{x^2}f'\left( x \right){\rm{d}}x} = 4 \Leftrightarrow \int\limits_0^1 {{x^2}{\rm{d}}\left( {f\left( x \right)} \right)} = \left. {{x^2}f\left( x \right)} \right|_0^1 - \int\limits_0^1 {2x \cdot f\left( x \right){\rm{d}}x = 4} \)
\[ \Leftrightarrow f\left( 1 \right) - 2 \cdot \int\limits_0^1 {x \cdot f\left( x \right){\rm{d}}x = 4} \Leftrightarrow \int\limits_0^1 {x \cdot f\left( x \right){\rm{d}}x = - 1} \].
Suy ra \(\int\limits_0^1 {\left( {7 - 3x} \right)\,} f\left( x \right){\rm{d}}x = 4 \Leftrightarrow 7 \cdot \int\limits_0^1 {f\left( x \right)} \,{\rm{d}}x - 3 \cdot \int\limits_0^1 {x \cdot f\left( x \right)} \,{\rm{d}}x = 4\)
\( \Leftrightarrow 7 \cdot \int\limits_0^1 {f\left( x \right)} \,{\rm{d}}x - 3 \cdot \left( { - 1} \right) = 4 \Leftrightarrow \int\limits_0^1 {f\left( x \right)} \,{\rm{d}}x = \frac{1}{7}\). Chọn D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\) là số hành khách trên mỗi chuyến xe để nhà xe thu được lợi nhuận lớn nhất.
Gọi \(F\left( x \right)\) là hàm chỉ số tiền thu được sau mỗi chuyến xe \(\left( {0 < x \le 60\,,\,\,x \in \mathbb{N}} \right).\)
Số tiền thu được sau mỗi chuyến xe:
\(F\left( x \right) = {\left( {300 - \frac{{5x}}{2}} \right)^2} \cdot x = 90\,\,000x - 1500{x^2} + \frac{{25}}{4}{x^3}\).
Bài toán trở thành tìm \(x\) để \(F(x)\) đạt giá trị lớn nhất thì \(F'\left( x \right) = 90\,\,000 - 3\,\,000x + \frac{{75}}{4}{x^2}\)
\(F'\left( x \right) = 0 \Leftrightarrow 90\,\,000 - 3\,\,000x + \frac{{75}}{4}{x^2} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 120}&{(L)}\\{x = 40}&{(TM)}\end{array}.} \right.\)
Bảng biến thiên:
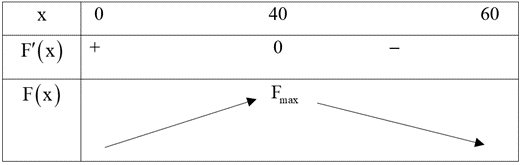
Vậy để thu được lợi nhuận của mỗi chuyến xe là lớn nhất thì mỗi chuyến xe phải chở 40 người.
Câu 2
Lời giải
Gọi \(H\) là hình chiếu vuông góc của \(A\left( {2\,;\,\, - 3\,;\,\,5} \right)\) lên \[Oy.\]
Suy ra \(H\left( {0\,;\,\, - 3\,;\,\,0} \right).\) Khi đó \(H\) là trung điểm đoạn \(AA'.\)
Do đó \[\left\{ {\begin{array}{*{20}{l}}{{x_H} = \frac{{{x_A} + {x_{A'}}}}{2}}\\{{y_H} = \frac{{{y_A} + {y_{A'}}}}{2}}\\{{z_H} = \frac{{{z_A} + {z_{A'}}}}{2}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_{A'}} = 2{x_H} - {x_A} = 2 \cdot 0 - 2 = - 2}\\{{y_{A'}} = 2{y_H} - {y_A} = 2 \cdot \left( { - 3} \right) - ( - 3) = - 3}\\{{z_{A'}} = 2{z_H} - {z_A} = 2 \cdot 0 - 5 = - 5}\end{array}} \right.} \right.\].
\[ \Rightarrow A'\left( { - 2\,;\,\, - 3\,;\,\, - 5} \right).\] Chọn D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.