Khi lai khác dòng thì con lai F1 có ưu thế lai cao nhất nhưng không dùng để nhân giống bằng phương pháp hữu tính vì
Quảng cáo
Trả lời:
Con lai \({F_1}\) có kiểu gen dị hợp, do đó nó có ưu thế lai cao, cho năng suất cao. Tuy nhiên, người ta không dùng giống có ưu thế lai để nhân giống vì khi nhân giống thì đời con sẽ phát sinh biến dị tổ hợp làm cho tỉ lệ dị hợp giảm dần và xuất hiện các đồng hợp lặn gây hại nên giống sẽ giảm năng suất. Chọn B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\) là số hành khách trên mỗi chuyến xe để nhà xe thu được lợi nhuận lớn nhất.
Gọi \(F\left( x \right)\) là hàm chỉ số tiền thu được sau mỗi chuyến xe \(\left( {0 < x \le 60\,,\,\,x \in \mathbb{N}} \right).\)
Số tiền thu được sau mỗi chuyến xe:
\(F\left( x \right) = {\left( {300 - \frac{{5x}}{2}} \right)^2} \cdot x = 90\,\,000x - 1500{x^2} + \frac{{25}}{4}{x^3}\).
Bài toán trở thành tìm \(x\) để \(F(x)\) đạt giá trị lớn nhất thì \(F'\left( x \right) = 90\,\,000 - 3\,\,000x + \frac{{75}}{4}{x^2}\)
\(F'\left( x \right) = 0 \Leftrightarrow 90\,\,000 - 3\,\,000x + \frac{{75}}{4}{x^2} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 120}&{(L)}\\{x = 40}&{(TM)}\end{array}.} \right.\)
Bảng biến thiên:
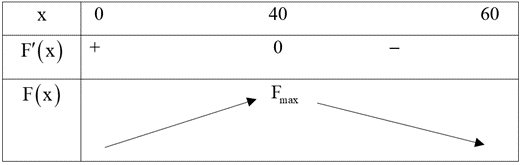
Vậy để thu được lợi nhuận của mỗi chuyến xe là lớn nhất thì mỗi chuyến xe phải chở 40 người.
Câu 2
Lời giải
Gọi \(H\) là hình chiếu vuông góc của \(A\left( {2\,;\,\, - 3\,;\,\,5} \right)\) lên \[Oy.\]
Suy ra \(H\left( {0\,;\,\, - 3\,;\,\,0} \right).\) Khi đó \(H\) là trung điểm đoạn \(AA'.\)
Do đó \[\left\{ {\begin{array}{*{20}{l}}{{x_H} = \frac{{{x_A} + {x_{A'}}}}{2}}\\{{y_H} = \frac{{{y_A} + {y_{A'}}}}{2}}\\{{z_H} = \frac{{{z_A} + {z_{A'}}}}{2}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_{A'}} = 2{x_H} - {x_A} = 2 \cdot 0 - 2 = - 2}\\{{y_{A'}} = 2{y_H} - {y_A} = 2 \cdot \left( { - 3} \right) - ( - 3) = - 3}\\{{z_{A'}} = 2{z_H} - {z_A} = 2 \cdot 0 - 5 = - 5}\end{array}} \right.} \right.\].
\[ \Rightarrow A'\left( { - 2\,;\,\, - 3\,;\,\, - 5} \right).\] Chọn D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.