Một lọ đựng dung dịch \({\rm{FeS}}{{\rm{O}}_4}\)(dung dịch X) để lâu ngày thì thấy màu của dung dịch chuyển sang màu vàng nâu.
Để xác định nồng độ ban đầu của \({\rm{FeS}}{{\rm{O}}_4}\), tiến hành như sau:
Thí nghiệm 1: thêm dung dịch \({\rm{NaOH}}\) từ từ tới dư vào \(50,00\;{\rm{mL}}\) dung dịch X thấy xuất hiện kết tủa, lọc kết tủa, làm khô cẩn thận thu được 4,67 g kết tủa.
Thí nghiệm 2: thêm từ từ dung dịch \({\rm{KMn}}{{\rm{O}}_4}0,50{\rm{M}}\) trong môi trường \({{\rm{H}}_2}{\rm{S}}{{\rm{O}}_4}\) vào \(50,00\;{\rm{mL}}\) dung dịch X, sau phản ứng thấy dùng hết \(16,00\;{\rm{mL}}\) dung dịch \({\rm{KMn}}{{\rm{O}}_4}.\)
Nồng độ ban đầu của \({\rm{FeS}}{{\rm{O}}_4}\) là
Một lọ đựng dung dịch \({\rm{FeS}}{{\rm{O}}_4}\)(dung dịch X) để lâu ngày thì thấy màu của dung dịch chuyển sang màu vàng nâu.
Để xác định nồng độ ban đầu của \({\rm{FeS}}{{\rm{O}}_4}\), tiến hành như sau:
Thí nghiệm 1: thêm dung dịch \({\rm{NaOH}}\) từ từ tới dư vào \(50,00\;{\rm{mL}}\) dung dịch X thấy xuất hiện kết tủa, lọc kết tủa, làm khô cẩn thận thu được 4,67 g kết tủa.
Thí nghiệm 2: thêm từ từ dung dịch \({\rm{KMn}}{{\rm{O}}_4}0,50{\rm{M}}\) trong môi trường \({{\rm{H}}_2}{\rm{S}}{{\rm{O}}_4}\) vào \(50,00\;{\rm{mL}}\) dung dịch X, sau phản ứng thấy dùng hết \(16,00\;{\rm{mL}}\) dung dịch \({\rm{KMn}}{{\rm{O}}_4}.\)
Nồng độ ban đầu của \({\rm{FeS}}{{\rm{O}}_4}\) là
A. \(1,25{\rm{M}}.\)
Quảng cáo
Trả lời:
Phân tích bài toán như sau:
Tại TN1: Kết tủa gồm \({\rm{Fe}}{({\rm{OH}})_2}\) và \({\rm{Fe}}{({\rm{OH}})_3}\)
\({\rm{FeS}}{{\rm{O}}_4} + 2{\rm{NaOH}} \to {\rm{Fe}}{({\rm{OH}})_2} \downarrow + {\rm{N}}{{\rm{a}}_2}{\rm{S}}{{\rm{O}}_4}\)
\({\rm{F}}{{\rm{e}}_2}{\left( {{\rm{S}}{{\rm{O}}_4}} \right)_3} + 6{\rm{NaOH}} \to 2{\rm{Fe}}{({\rm{OH}})_3} \downarrow + 3{\rm{N}}{{\rm{a}}_2}{\rm{S}}{{\rm{O}}_4}\)
Tại TN2: Chỉ có muối sắt (II) mới làm mất màu dung dịch \({\rm{KMn}}{{\rm{O}}_4}\) trong môi trường \({{\rm{H}}_2}{\rm{S}}{{\rm{O}}_4}.\)
\({n_{{\rm{KMn}}{{\rm{O}}_4}}} = 0,5 \cdot \frac{{16}}{{1000}} = {8.10^{ - 3}}\;{\rm{mol}}\)
Phương trình hóa học:
\(\begin{array}{l}10{\rm{FeS}}{{\rm{O}}_4} + 2{\rm{KMn}}{{\rm{O}}_4} + 8{{\rm{H}}_2}{\rm{S}}{{\rm{O}}_4} \to 5{\rm{F}}{{\rm{e}}_2}{\left( {{\rm{S}}{{\rm{O}}_4}} \right)_3} + {{\rm{K}}_2}{\rm{S}}{{\rm{O}}_4} + 2{\rm{MnS}}{{\rm{O}}_4} + 8{{\rm{H}}_2}{\rm{O}}\\0,04\,\,\,\, \leftarrow {8.10^{ - 3}}\;{\rm{mol}}\end{array}\)
Þ \({{\rm{n}}_{{\rm{FeS}}{{\rm{O}}_4}}} = 0,04\) mol \( \Rightarrow {n_{Fe{{(OH)}_2}\,\,(TN1)}} = {n_{FeS{O_4}}} = 0,04\,mol\)
Ở TN1, thu được 4,67 gam kết tủa nên ta có:
4,67 = 0,04.90 + \({n_{Fe{{(OH)}_3}}} \cdot 107 \Rightarrow {n_{Fe{{(OH)}_3}}} = 0,01\,mol\)
Bảo toàn nguyên tố \(({\rm{Fe}})\) ta có:
Nồng độ ban đầu của \({\rm{FeS}}{{\rm{O}}_4}\) là \( = \frac{{0,05}}{{0,05}} = 1M\)
Chọn C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\) là số hành khách trên mỗi chuyến xe để nhà xe thu được lợi nhuận lớn nhất.
Gọi \(F\left( x \right)\) là hàm chỉ số tiền thu được sau mỗi chuyến xe \(\left( {0 < x \le 60\,,\,\,x \in \mathbb{N}} \right).\)
Số tiền thu được sau mỗi chuyến xe:
\(F\left( x \right) = {\left( {300 - \frac{{5x}}{2}} \right)^2} \cdot x = 90\,\,000x - 1500{x^2} + \frac{{25}}{4}{x^3}\).
Bài toán trở thành tìm \(x\) để \(F(x)\) đạt giá trị lớn nhất thì \(F'\left( x \right) = 90\,\,000 - 3\,\,000x + \frac{{75}}{4}{x^2}\)
\(F'\left( x \right) = 0 \Leftrightarrow 90\,\,000 - 3\,\,000x + \frac{{75}}{4}{x^2} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 120}&{(L)}\\{x = 40}&{(TM)}\end{array}.} \right.\)
Bảng biến thiên:
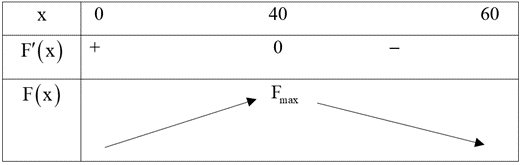
Vậy để thu được lợi nhuận của mỗi chuyến xe là lớn nhất thì mỗi chuyến xe phải chở 40 người.
Câu 2
Lời giải
Gọi \(H\) là hình chiếu vuông góc của \(A\left( {2\,;\,\, - 3\,;\,\,5} \right)\) lên \[Oy.\]
Suy ra \(H\left( {0\,;\,\, - 3\,;\,\,0} \right).\) Khi đó \(H\) là trung điểm đoạn \(AA'.\)
Do đó \[\left\{ {\begin{array}{*{20}{l}}{{x_H} = \frac{{{x_A} + {x_{A'}}}}{2}}\\{{y_H} = \frac{{{y_A} + {y_{A'}}}}{2}}\\{{z_H} = \frac{{{z_A} + {z_{A'}}}}{2}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_{A'}} = 2{x_H} - {x_A} = 2 \cdot 0 - 2 = - 2}\\{{y_{A'}} = 2{y_H} - {y_A} = 2 \cdot \left( { - 3} \right) - ( - 3) = - 3}\\{{z_{A'}} = 2{z_H} - {z_A} = 2 \cdot 0 - 5 = - 5}\end{array}} \right.} \right.\].
\[ \Rightarrow A'\left( { - 2\,;\,\, - 3\,;\,\, - 5} \right).\] Chọn D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.