Trong không gian Oxyz, tính góc giữa đường thẳng D và mặt phẳng (P), với: , (P): x – y + z – 1 = 0.
Trong không gian Oxyz, tính góc giữa đường thẳng D và mặt phẳng (P), với: , (P): x – y + z – 1 = 0.
Quảng cáo
Trả lời:
Đường thẳng D có vectơ chỉ phương là \(\overrightarrow u = \left( { - 1;2;1} \right)\).
Mặt phẳng (P) có vectơ pháp tuyến là \(\overrightarrow n = \left( {1; - 1;1} \right)\).
Ta có \(\sin \left( {\Delta ,\left( P \right)} \right) = \frac{{\left| { - 1 - 2 + 1} \right|}}{{\sqrt {{{\left( { - 1} \right)}^2} + {2^2} + {1^2}} .\sqrt {{1^2} + {{\left( { - 1} \right)}^2} + {1^2}} }} = \frac{2}{{3\sqrt 2 }}\).
Do đó (D, (P)) ≈ 28,1°.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Sau khi học xong bài này, ta giải quyết bài toán này như sau:
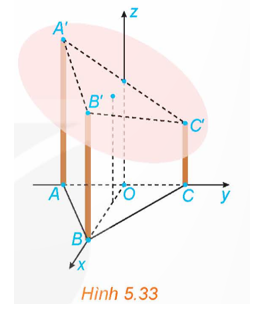
Chọn hệ trục tọa độ như hình vẽ với O là trung điểm của AC.
Ta có: A(0; −2; 0), B(\(2\sqrt 3 \); 0; 0), C(0; 2; 0), A'(0; −2; 7), B'(\(2\sqrt 3 \); 0; 6), C'(0; 2; 5).
Ta có \(\overrightarrow {AB} = \left( {2\sqrt 3 ;2;0} \right),\overrightarrow {AC} = \left( {0;4;0} \right),\overrightarrow {A'B'} = \left( {2\sqrt 3 ;2; - 1} \right),\overrightarrow {A'C'} = \left( {0;4; - 2} \right)\).
Có \(\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}2&0\\4&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}0&{2\sqrt 3 }\\0&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{2\sqrt 3 }&2\\0&4\end{array}} \right|} \right)\) \( = \left( {0;0;8\sqrt 3 } \right)\).
\(\left[ {\overrightarrow {A'B'} ,\overrightarrow {A'C'} } \right] = \left( {\left| {\begin{array}{*{20}{c}}2&{ - 1}\\4&{ - 2}\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{ - 1}&{2\sqrt 3 }\\{ - 2}&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{2\sqrt 3 }&2\\0&4\end{array}} \right|} \right)\)\( = \left( {0;4\sqrt 3 ;8\sqrt 3 } \right)\).
Mặt phẳng (ABC) có một vectơ pháp tuyến là \(\frac{1}{{8\sqrt 3 }}\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {0;0;1} \right)\).
Mặt phẳng (A'B'C') có một vectơ pháp tuyến là \(\frac{1}{{4\sqrt 3 }}\left[ {\overrightarrow {A'B'} ,\overrightarrow {A'C'} } \right] = \left( {0;1;2} \right)\).
Do đó \(\cos \left( {\left( {ABC} \right),\left( {A'B'C'} \right)} \right) = \frac{{\left| 2 \right|}}{{\sqrt 1 .\sqrt {1 + 4} }} = \frac{2}{{\sqrt 5 }}\)Þ ((ABC), (A'B'C')) ≈ 26,6°.
Suy ra mái nhà nghiêng với mặt sàn nhà một góc khoảng 26,6°.
Lời giải
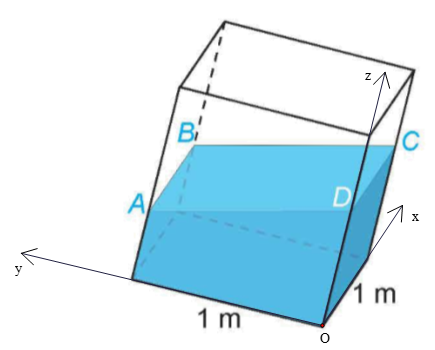
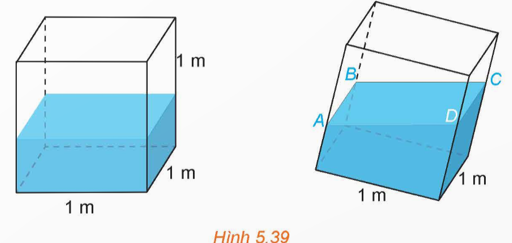
a) Chọn hệ trục tọa độ như hình vẽ.
40 cm = 0,4 m, 44 cm = 0,44 m, 48 cm = 0,48 m.
Khi đó ta có A(0; 1; 0,4), B(1; 1; 0,44), C(1; 0; 0,48).
Có \(\overrightarrow {AB} = \left( {1;0;0,04} \right)\).
Vì ABCD là hình bình hành nên \(\overrightarrow {AB} = \overrightarrow {DC} \)\( \Leftrightarrow \left\{ \begin{array}{l}1 - {x_D} = 1\\ - {y_D} = 0\\0,48 - {z_D} = 0,04\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 0\\{y_D} = 0\\{z_D} = 0,44\end{array} \right.\).
Suy ra D(0; 0; 0,44).
Vậy khoảng cách từ điểm D đến đáy bể là 44 cm.
b) Ta có đáy bể nằm trong mặt phẳng Oxy: z = 0 có vectơ pháp tuyến \(\overrightarrow k = \left( {0;0;1} \right)\).
Ta có\(\overrightarrow {AB} = \left( {1;0;0,04} \right)\), \(\overrightarrow {AC} = \left( {1; - 1;0,08} \right)\), \(\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {0,04; - 0,04; - 1} \right)\).
Mặt phẳng (ABCD) đi qua A(0; 1; 0,4) và có vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {0,04; - 0,04; - 1} \right)\) có phương trình là:
0,04x – 0,04(y – 1) – (z – 0,4) = 0 Û 0,04x – 0,04y – z + 0,44 = 0.
Do đó góc giữa đáy bể và mặt phẳng nằm ngang chính là góc giữa mặt phẳng (ABCD) và mặt đáy.
Có \(\cos \left( {\left( {ABCD} \right),\left( {Oxy} \right)} \right) = \frac{{\left| { - 1} \right|}}{{\sqrt 1 .\sqrt {{{0,04}^2} + {{\left( { - 0,04} \right)}^2} + {{\left( { - 1} \right)}^2}} }}\) \( = \frac{{25}}{{\sqrt {627} }}\).
Suy ra ((ABCD), (Oxy)) ≈ 3,2°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.