Câu hỏi:
12/07/2024 65
Cho hình lăng trụ \(ABC.A'B'C'\) có \(\widehat {AA'B} = \widehat {BA'C} = \widehat {CA'A} = 60^\circ .\) Biết \(AA' = 3\sqrt 2 \,,\,\,BA' = 4\sqrt 2 \), \(CA' = 5\sqrt 2 .\) Thể tích của khối lăng trụ \(ABC.A'B'C'\) bằng
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
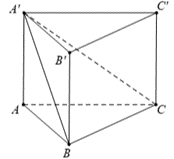
Áp dụng công thức tính nhanh sau:
Cho khối chóp \[S.ABC\]. Đặt \(SA = a\,,\,\,SB = b\,,\,\,SC = c\,,\,\,\widehat {BSC} = \alpha \,,\,\,\widehat {CSA} = \beta \,,\,\,\widehat {ASB} = \lambda .\)
Khi đó ta có: \({V_{S.ABC}} = \frac{1}{6}abc\sqrt {1 + 2\cos \alpha \cos \beta \cos \lambda - {{\cos }^2}\alpha - {{\cos }^2}\beta - {{\cos }^2}\lambda } \).
Đặt \(\widehat {AA'B} = \widehat {BA'C} = \widehat {CA'A} = \alpha = 60^\circ .\)
Ta có \({V_{A'.ABC}} = \frac{1}{6}AA' \cdot A'B \cdot A'C \cdot \sqrt {1 + 2{{\cos }^3}\alpha - 3{{\cos }^2}\alpha } = 20.\)
Suy ra thể tích khối lăng trụ \(ABC.A'B'C'\) bằng:
\[{V_{ABC.A'B'{{C'}^\prime }}} = 3{V_{A' \cdot ABC}} = 3 \cdot 20 = 60.\]
Đáp án: 60.Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số Biết rằng đồ thị hàm số đã cho đi qua điểm \(\left( { - 1\,;\,\,7} \right)\) và giao điểm hai đường tiệm cận là \(\left( { - 2\,;\,\,3} \right).\) Giá trị của biểu thức \(\frac{{2a + 3b + 4c + d}}{{7c}}\) bằng\(f\left( x \right) = \frac{{ax + b}}{{cx + d}}\,\,\left( {a,\,\,b,\,\,c,\,\,d \in \mathbb{R},\,\,c \ne 0} \right).\)
Xem đáp án »
26/06/2024
4,668
Câu 2:
Có bao nhiêu giá trị nguyên của tham số \[m \in \left[ { - 10\,;\,\,10} \right]\] để đồ thị hàm số \(y = \frac{{x - 1}}{{2{x^2} + 6x - m - 3}}\) có hai đường tiệm cận đứng?
Có bao nhiêu giá trị nguyên của tham số \[m \in \left[ { - 10\,;\,\,10} \right]\] để đồ thị hàm số \(y = \frac{{x - 1}}{{2{x^2} + 6x - m - 3}}\) có hai đường tiệm cận đứng?
Xem đáp án »
13/07/2024
4,115
Câu 3:
Trong không gian \[Oxyz,\] cho bốn điểm \[A\left( {1\,;\,\, - 2\,;\,\,0} \right),\,\,B\left( {2\,;\,\,0\,;\,\,3} \right),\]\[C\left( { - 2\,;\,\,1\,;\,\,3} \right),\]\[D\left( {0\,;\,\,1\,;\,\,1} \right)\]. Thể tích khối tứ diện \[ABCD\] bằng
Trong không gian \[Oxyz,\] cho bốn điểm \[A\left( {1\,;\,\, - 2\,;\,\,0} \right),\,\,B\left( {2\,;\,\,0\,;\,\,3} \right),\]\[C\left( { - 2\,;\,\,1\,;\,\,3} \right),\]\[D\left( {0\,;\,\,1\,;\,\,1} \right)\]. Thể tích khối tứ diện \[ABCD\] bằng
Xem đáp án »
26/06/2024
3,571
Câu 4:
Có bao nhiêu giá trị nguyên của tham số \(m \in \left[ { - 20\,;\,\,20} \right]\) để hàm số \(y = - {x^4} + 6{x^2} + \left( {m - 2} \right)x + 3\) có đúng một điểm cực trị?
Có bao nhiêu giá trị nguyên của tham số \(m \in \left[ { - 20\,;\,\,20} \right]\) để hàm số \(y = - {x^4} + 6{x^2} + \left( {m - 2} \right)x + 3\) có đúng một điểm cực trị?
Xem đáp án »
26/06/2024
1,870
Câu 5:
Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = \frac{m}{3}{x^3} - 2m{x^2} + \left( {3m + 5} \right)x\) đồng biến trên \(\mathbb{R}\)?
Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = \frac{m}{3}{x^3} - 2m{x^2} + \left( {3m + 5} \right)x\) đồng biến trên \(\mathbb{R}\)?
Xem đáp án »
26/06/2024
1,764
Câu 6:
Trong không gian \[Oxyz,\] phương trình mặt cầu đi qua điểm \[A\left( {1\,;\,\, - 1\,;\,\,4} \right)\] và tiếp xúc với các mặt phẳng tọa độ là
Xem đáp án »
26/06/2024
1,019
Câu 7:
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \frac{1}{{x - 1}} + 6x\,,\,\,\forall x \in \left( {1\,;\,\, + \infty } \right)\) và \(f(2) = 12.\) Biết \(F\left( x \right)\) là nguyên hàm của \(f\left( x \right)\) thỏa mãn \(F(2) = 6\), khi đó giá trị biểu thức \(F\left( 5 \right) - 4F\left( 3 \right)\) bằng
Xem đáp án »
26/06/2024
853
về câu hỏi!