Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 16)
83 người thi tuần này 4.6 2.6 K lượt thi 150 câu hỏi 150 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 45)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 44)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 43)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 42)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 41)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 40)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 39)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 38)
Danh sách câu hỏi:
Câu 1
A. Đại học.
B. Cao đẳng.
Lời giải
Nhu cầu tuyển dụng lao động theo trình độ trong 6 tháng đầu năm 2018 ở trình độ lao động phổ thông là cao nhất \[\left( {66\% } \right).\] Chọn D.
Câu 2
A. \(m = 7,\,\,n = - \frac{3}{4}.\)
B. \(m = 4,\,\,n = - 3.\)
Lời giải
Ta thấy \(\vec a\) và \(\vec b\) cùng hướng \( \Leftrightarrow \vec a = k\vec b\,\,(k > 0) \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2 = k}\\{m - 1 = 3k}\\{3 = k\left( { - 2n} \right)}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{k = 2}\\{m = 7\,;\,\,n = - \frac{3}{4}}\end{array}} \right.} \right..\)
Vậy \(m = 7\,;\,\,n = - \frac{3}{4}.\) Chọn A.
Câu 3
Lời giải
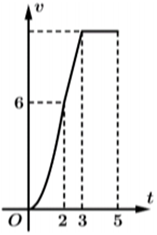
Ta có \(v(t) = S'(t) = 4{t^3} - 18t - 21\).
Do đó, vận tốc của chuyển động tại thời điểm \(t = 3\) giây là:
\(v(3) = {4.3^3} - 18.3 - 21 = 33\,\,(\;{\rm{m}}/{\rm{s}}).\) Chọn C.
Câu 4
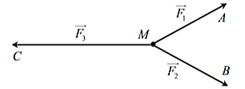
A. \(50\sqrt 3 \,N.\)
Lời giải
Do vật đứng yên nên tổng hợp lực tác động vào vật bằng 0.
\(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \vec 0 \Leftrightarrow \overrightarrow {{F_1}} + \overrightarrow {{F_2}} = - \overrightarrow {{F_3}} \Rightarrow \left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right|{\rm{. }}\)
Lại có \({\left( {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right)^2} = {\overrightarrow {{F_1}} ^2} + 2 \cdot \overrightarrow {{F_1}} \cdot \overrightarrow {{F_2}} + {\overrightarrow {{F_2}} ^2} = F_1^2 + 2 \cdot {F_1} \cdot {F_2} \cdot \cos \widehat {AMB} + F_2^2\)
Khi đó \({\left( {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right)^2} = 2 \cdot {100^2} + 2 \cdot {100^2} \cdot \cos 60^\circ = 3 \cdot {100^2}\)\( \Leftrightarrow \left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right| = 100\sqrt 3 {\rm{.}}\)
Vậy \(\left| {\overrightarrow {{F_3}} } \right| = 100\sqrt 3 .\) Chọn C.
Câu 5
Lời giải
Ta có \(\left( {1 + i} \right)z + 2\bar z = 3 + 2i\)\( \Leftrightarrow \left( {1 + i} \right)\left( {a + bi} \right) + 2\left( {a - bi} \right) = 3 + 2i\)
\( \Leftrightarrow a + bi + ai - b + 2a - 2bi = 3 + 2i\)\( \Leftrightarrow 3a - b + \left( {a - b} \right)i = 3 + 2i\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{3a - b = 3}\\{a - b = 2}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = \frac{1}{2}}\\{b = - \frac{3}{2}}\end{array}} \right.} \right.\).
Vậy \(P = a + b = - 1.\) Chọn D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. \(90^\circ .\)
B. \(30^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
A. 18
B. 20
C. 19
D. 21
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
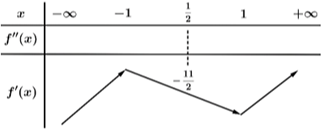
A. 1 điểm cực đại và 2 điểm cực tiểu.
B. 1 điểm cực đại và 3 điểm cực tiểu.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
A. \[{\left( {x - 3} \right)^2} + {\left( {y + 3} \right)^2} + {\left( {z + 3} \right)^2} = 16.\]
B. \({\left( {x - 3} \right)^3} + {\left( {y + 3} \right)^2} + {\left( {z - 3} \right)^2} = 9.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 28
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 29
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 30
A. \(3x + 2y + z + 14 = 0.\)
B. \(2x + y + 3z + 9 = 0.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 33
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 35
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 51
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 52
A. giọt nước.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 53
A. chúa đất áp bức.
B. cuộc sống tăm tối.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 54
A. kiêu hãnh.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 55
A. đã.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 56
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 57
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 58
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 59
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 60
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 61
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 62
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 63
A. tự sự.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 65
A. kế thừa – phát huy.
B. kế cận – sáng tạo.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 66
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 67
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 68
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 70
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 71
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 72
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 73
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 74
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 75
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 77
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 78
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 79
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 80
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 82
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 83
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 84
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 85
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 86
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 87
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 88
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 89
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 90
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 91
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 92
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 93
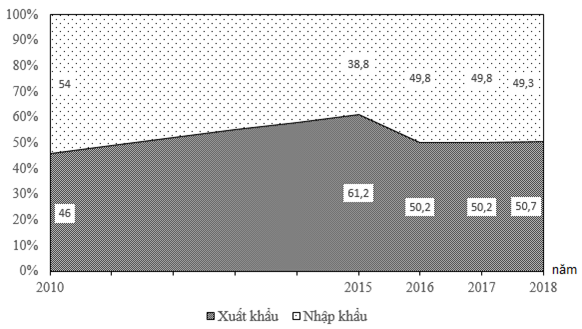
A. Tốc độ tăng trưởng giá trị xuất nhập khẩu của nước ta giai đoạn 2010-2018.
B. Chuyển dịch cơ cấu giá trị xuất nhập khẩu của nước ta giai đoạn 2010-2018.
C. Giá trị xuất nhập khẩu của nước ta giai đoạn 2010-2018.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 94
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 95
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 96
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 97
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 98
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 99
A. 2.10-7 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 100
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 101
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 102
A. \(0,{96.10^{ - 3}}{\mkern 1mu} {\mkern 1mu} \left( T \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 103
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 104
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 105
A. cùng biên độ và cùng pha.
B. khác biên độ và cùng pha.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 106
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 108
A. \[{C_4}{H_{10}}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 109
A. 29,51 gam.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 110
A. 12,18%.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 111
A. 3,12.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 113
A. 10%.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 114
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 116
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 118
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 119
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 120
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 121
A. (1).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 122
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 124
A. 100% Bb.
B. 100% bb.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 125
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 1
Đọc đoạn trích sau và trả lời các câu hỏi từ 51 đến 55:
(1) Hôm rồi tôi có dịp ghé nhà một ông tá hải quân cùng quê chơi. Ông hiện phụ trách quân lực của cả một vùng. Ông vừa cất xong ngôi nhà (biệt thự thì đúng hơn) và sắm xe hơi mới. Bước vào phòng khách ngôi nhà, ập vào mắt tôi chính là chiếc tủ rượu hoành tráng được gắn sát chiếm diện tích gần nửa bức tường chính diện. Thôi thì đủ thương hiệu rượu danh tiếng: từ Chivas, Hennessy, Napoleon, Johnnie Walker cho tới Vodka xịn tận bên Nga... được gia chủ bày khá ngay ngắn trên kệ. Ông đi giới thiệu cho chúng tôi xuất xứ từng chai rượu: chai này thằng bạn đi nước ngoài về tặng, chai kia đồng nghiệp cho, chai nọ do cấp dưới biếu với giọng khá hào hứng cũng như thể hiện sự am hiểu về rượu ngoại....
(2) Câu chuyện thứ hai tôi muốn đề cập với các bạn thói quen đọc sách của người Do Thái. “Trong mỗi gia đình Do Thái luôn luôn có một tủ sách được truyền từ đời này sang đời khác. Tủ sách phải được đặt ở vị trí đầu giường để trẻ nhỏ dễ nhìn, dễ thấy từ khi còn nằm nôi. Để sách hấp dẫn trẻ, phụ huynh Do Thái thường nhỏ nước hoa lên sách để tạo mùi hương cho các em chú ý”. Tác giả Nguyễn Hương trong bài “Người Việt ít đọc sách: Cần những chính sách để thay đổi toàn diện” (đăng trên trang tin điện tử Cinet.com của Bộ VH-TT-DL) kể với chúng ta như vậy.
(3) Câu chuyện về cái “tủ rượu” của ông tá hải quân trong câu chuyện đầu bài và cái “tủ sách” của người Do Thái, hay câu chuyện “văn hóa đọc” của người Việt Nam có mối liên hệ chặt chẽ với khoảng cách phát triển hiện tại giữa chúng ta với thế giới. Để đất nước và con người Việt Nam phát triển về mọi mặt, bền vững, việc đầu tiên là phải làm sao để “văn hóa đọc” của người Việt lan tỏa và thăng hoa, tạo thói quen đọc sách và yêu sách. Muốn phát triển như Âu -Mỹ, Nhật hay người Do Thái, trước hết phải học hỏi văn hóa đọc từ họ. Phải làm sao nhà nhà đều có “tủ sách” để tự hào và gieo hạt, chứ không phải là “tủ rượu” để khoe mẽ vật chất và phô trương cái tư duy trọc phú. Mọi thay đổi phải bắt đầu từ thế hệ trẻ.
(Tủ rượu của người Việt và tủ sách của người Do Thái - Báo điện tử vanhoagiaoduc.vn)
Câu 128
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 129
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 130
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 131
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 132
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 2
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 56 đến 60:
Ôi quê hương xanh biếc bóng dừa
Có ngờ đâu hôm nay ta trở lại
Quê hương ta tất cả vẫn còn đây
Dù người thân đã ngã xuống đất này
Ta gặp lại những mặt người ta yêu biết mấy
Ta nhìn, ta ngắm, ta say
Ta run run nắm những bàn tay
Thương nhớ dồn trong tay ta nóng bỏng
Đây rồi đoạn đường xưa
Nơi ta vẫn thường đi trong mộng
Kẽo kẹt nhà ai tiếng võng đưa
Ầu ơ...thương nhớ lắm!
Ơi những bông trang trắng, những bông trang hồng
Như tấm lòng em trong trắng thủy chung
Như trái tim em đẹp màu đỏ thắm
Con sông nhỏ tuổi thơ ta đã tắm
Vẫn còn đây nước chẳng đổi dòng
Hoa lục bình tím cả bờ sông
(Trở về quê nội – Lê Anh Xuân)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 134
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 135
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 136
A. So sánh.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 137
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 61 đến 65:
Từ bề sâu địa chất với số đo vạn triệu năm, ta lại trở về với bề mặt địa lí Hà Nội, với số đo nghìn năm trở lại. Nét địa lí trường tồn của nghìn xưa Thăng Long và hôm nay Hà Nội, đó là cái đặc trưng của thành phố sông: thành phố ngã ba sông, nếu lấy cả hai dòng Hồng Hà - Tô Lịch làm hệ quy chiếu, làm trục chủ đạo; thành phố một bờ sông (bờ phải) nếu chỉ lấy một sông Hồng làm trục chính. Một điều hiển nhiên, đất Hà Nội là đất bãi, và trên bãi của sông Hồng, do phù sa sông Hồng đắp nổi mà nên. Nhưng sự đắp đổi, trải mấy nghìn năm đã diễn ra không đơn giản: Có đời sống du đãng tự nhiên của những con sông ở đồng bằng do chính chúng tạo thành - đổi dòng từ từ hay khi có đột biến, có sự can thiệp, hữu thức và vô thức của con người. Thục Phán đắp lũy thành Cổ Loa cũng là đắp đê phòng lụt. Sử biên niên nhà Hán chép rằng, ở đầu công nguyên, huyện Phong Khê (Đông Anh) đã có đê phòng lụt. Đê sẽ làm cho quá trình bồi tụ tự nhiên bị ngăn chặn lại, ít nhất là từng phần. Cho nên đất Hà Nội nội thành, bên hồ Tây và dòng Tô Lịch, lại có rất nhiều đầm hồ. Xem trên các bản đồ từ thời xưa cho đến giữa thế kỉ này, thì thấy lãnh thổ Hà Nội là một vùng đầm lầy, một thành phố sông hồ, nửa đất, nửa nước. Quy hoạch Hà Nội cổ là nương theo và thích ứng đến mức tối đa cái hình thể tự nhiên của sông hồ đó. Phần lãnh thổ chủ yếu của Thăng Long - Hà Nội xưa là phần đất bồi, được bao bọc bởi sông Hồng ở phía Bắc và phía Đông, bờ sông Tô Lịch và sông Kim Ngưu (nhánh sông Tô) ở phía tây và phía nam. Lũy bọc ngoài đê mà cũng là thành đất, là đường giao thông (đê La Thành). Sông hồ không những là nguồn nước dùng trong sinh hoạt mà còn là hệ thống thuỷ lợi và giao thông truyền thống. Sông hồ cũng là những sự kiện địa lí được dùng làm nguyên lí sơ khởi chỉ đạo việc quy tụ xóm làng, phường và thành lũy phòng vệ (sử dụng những đoạn sông Hồng, sông Tô làm ngoại hào). Dân gian Hà Nội xưa đã khái quát về khoảnh đất cốt lõi của Hà Nội cổ, của kinh thành cổ kính:
Nhị Hà quanh bắc sang đông,
Kim Ngưu, Tô Lịch là sông bên này.
(Trần Quốc Vượng, Trên mảnh đất nghìn năm văn vật, NXB Hà Nội, 2009, Tr.21)
Câu 138
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 139
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 140
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 141
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 142
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 66 đến 70:
Em trở về đúng nghĩa trái tim em
Biết khao khát những điều anh mơ ước
Biết xúc động qua nhiều nhận thức
Biết yêu anh và biết được anh yêu
Mùa thu nay sao bão mưa nhiều
Những cửa sổ con tàu chẳng đóng
Dải đồng hoang và đại ngàn tối sẫm
Em lạc loài giữa sâu thẳm rừng anh.
(Trích Tự hát – Xuân Quỳnh)
Câu 143
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 144
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 145
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 146
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 147
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 5
Dựa vào các thông tin sau đây để trả lời các câu hỏi từ câu 108 đến câu 110:
"Tháng 3-1947, Chính phủ Pháp cử Bôlae làm Cao uỷ Pháp ở Đông Dương, thực hiện kế hoạch tiến công căn cứ địa Việt Bắc nhằm nhanh chóng kết thúc chiến tranh.
Thực dân Pháp huy động 12000 quân và hầu hết máy Bay ở Đông Dương mở cuộc tiến công Việt Bắc từ ngày 7-10-1947.
Sáng sớm 7-10-1947, binh đoàn quân dù do Sôvanhăc chỉ huy đổ quân xuống chiếm thị xã Bắc Kạn, thị trấn Chợ Mới,... Cùng ngày, binh đoàn bộ binh do Bôphơrê chủ huy, tử Lạng Sơn theo Đường số 4 đánh lên Cao Bằng, rồi vòng xuống Bắc Kạn theo Đường số 3 , Bao vây Việt Bắc ở phía đông và phía Bắc Ngày 9-10-1947, một binh đoàn hổn hợp bộ binh và lính thủy đánh bộ do Cômmuynan chỉ huy từ Hà Nội đi ngược sông Hồng và sông Lô lên Tuyên Quang, rồi Chiêm Hóa, đánh vào Đài Thị, Bao vây Việt Bắc ở phía tây.
Khi địch vừa tiến công Việt Bắc, Đảng ta đã có chỉ thị "Phải phá tan cuộc tiến công mùa đông của giặc Pháp". Trên khắp các mặt trận, quân dân ta anh dũng chiến đấu, từng Bước đẩy lùi cuộc tiến công của địch.
Quân dân ta chủ Bao vây tiến công địch Chợ Mới, Chợ Đồn, Chợ Rã, Ngân Sơn, Bạch Thông (nay thuộc Bắc Kạn) v.v., Buộc Pháp phải Chợ Đồn, Chợ Rã cuối tháng 11-1947.
Ở mặt trận hướng đông, quân dân ta phục kích chặn đánh địch trên Đường số 4, tiêu biểu là trận phục kích đèo Bông Lau (30-10-1947), đánh trúng đoàn cơ giới của địch, thu nhiều khí, quân trang quân dụng của chúng.
Ở mặt trận hướng tây, quân dân ta phục kích đánh địch nhiều trên sông Lô, nổi bật là trận Đoan Hùng, Khe Lau, đánh chìm nhiều tàu chiến, ca nô của địch.
Sau hơn hai tháng, cuộc chiến đấu giữa địch thúc bằng cuộc rút chạy của đại bộ phận quân Pháp khỏi Việt Bắc ngày 19-12-1947.
Quân dân ta loại khỏi vòng chiến đấu hơn 6000 địch, bắn rơi 16 máy Bay, bắn chìm 11 tàu chiến, ca nô, phá huỷ nhiều phương tiện chiến tranh. Cơ quan đầu não kháng chiến được bảo toàn. Bộ đội chủ lực của ta ngày càng trưởng thành.
Với chiến thắng Việt Bắc thu-đông năm 1947, cuộc kháng chiến toàn quốc chống thực dân Pháp xâm lược chuyển sang giai đoạn mới.
Sau thất bại ở Việt Bắc, Pháp Buộc phải thay đổi chiến lược chiến tranh ở Đông Dương, từ "đánh nhanh, thắng nhanh" sang "đánh lâu dài", thực hiện chính sách "dùng người Việt đánh người Việt, lấy chiến tranh nuôi chiến tranh".
(Nguồn: SGK Lịch sử 12, NXB Giáo dục Việt Nam, 2023, trang 133-134)
Câu 148
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 149
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 150
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

![Cho một lá iron nhỏ tác dụng với dung dịch \[{H_2}S{O_4}.\]Thể tích khí \[{H_2}\] thu được tương ứng với thời gian đo được như sau: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/07/blobid9-1721815075.png)