Câu hỏi:
24/07/2024 53
Đặt vào hai đầu đoạn mạch RLC mắc nối tiếp (cuộn dây thuần cảm, tụ điện có điện dung C thay đổi được) một điện áp xoay chiều \(u = U\sqrt 2 \cos \omega {\rm{t}}\) (V). Trong đó U và \(\omega \) không đổi. Cho C biến thiên thu được đồ thị biểu diễn điện áp trên tụ theo dung kháng \({{\rm{Z}}_{\rm{C}}}\) như hình vẽ. Coi \(72,11 = 20\sqrt {13} .\) Điện trở của mạch là
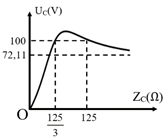
Đặt vào hai đầu đoạn mạch RLC mắc nối tiếp (cuộn dây thuần cảm, tụ điện có điện dung C thay đổi được) một điện áp xoay chiều \(u = U\sqrt 2 \cos \omega {\rm{t}}\) (V). Trong đó U và \(\omega \) không đổi. Cho C biến thiên thu được đồ thị biểu diễn điện áp trên tụ theo dung kháng \({{\rm{Z}}_{\rm{C}}}\) như hình vẽ. Coi \(72,11 = 20\sqrt {13} .\) Điện trở của mạch là
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hiệu điện thế giữa hai đầu tụ điện là:
\({U_C} = I.{Z_C} = \frac{{U{Z_C}}}{Z} = \frac{{U{Z_C}}}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \frac{{U{Z_C}}}{{\sqrt {{{\left( {{R^2} + {Z_L}} \right)}^2} - 2{Z_L}{Z_C} + {Z_C}^2} }}\)
\( \Rightarrow {U_C} = \frac{U}{{\sqrt {\left( {{R^2} + {Z_L}^2} \right)\frac{1}{{{Z_C}^2}} - 2{Z_L}\frac{1}{{{Z_C}}} + 1} }}{\mkern 1mu} {\mkern 1mu} \left( 1 \right)\)
Từ (1), ta có: \(\left( {{R^2} + {Z_L}^2} \right)\frac{1}{{{Z_C}^2}} - 2{Z_L}\frac{1}{{{Z_C}}} + 1 - {\left( {\frac{U}{{{U_C}}}} \right)^2} = 0\) (*)
Với giá trị của dung kháng \(\left\{ {\begin{array}{*{20}{l}}{{Z_{{C_1}}} = \frac{{125}}{3}{\mkern 1mu} {\mkern 1mu} \Omega }\\{{Z_{{C_2}}} = 125{\mkern 1mu} {\mkern 1mu} \Omega }\end{array}} \right.\), cho cùng 1 giá trị hiệu điện thế: \({U_{{C_1}}} = {U_{{C_2}}} = 100{\mkern 1mu} {\mkern 1mu} \left( V \right)\)
Khi \({Z_C} \to \infty \) thì \({U_C} = U = 72,11{\mkern 1mu} {\mkern 1mu} V = 20\sqrt {13} {\mkern 1mu} {\mkern 1mu} V\)\( \Rightarrow 1 - {\left( {\frac{U}{{{U_C}}}} \right)^2} = 1 - {\left( {\frac{{20\sqrt {13} }}{{100}}} \right)^2} = 0,48\)
\( \Rightarrow \left( {{R^2} + {Z_L}^2} \right)\frac{1}{{{Z_C}^2}} - 2{Z_L}\frac{1}{{{Z_C}}} + 0,48 = 0\)
Theo định lí Vi – et, đặt \[x = \frac{1}{{{Z_C}}}\] ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = \frac{{ - b}}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\frac{1}{{{Z_{{C_1}}}}} + \frac{1}{{{Z_{{C_2}}}}} = \frac{{2{Z_L}}}{{{R^2} + {Z_L}^2}}}\\{\frac{1}{{{Z_{{C_1}}}}}.\frac{1}{{{Z_{{C_2}}}}} = \frac{{0,48}}{{{R^2} + {Z_L}^2}}}\end{array}} \right.\)
\( \Rightarrow {R^2} + {Z_L}^2 = \frac{{0,48}}{{\frac{1}{{{Z_{{C_1}}}}}.\frac{1}{{{Z_{{C_2}}}}}}} = \frac{{0,48}}{{\frac{1}{{\frac{{125}}{3}}}.\frac{1}{{125}}}} = 2500\)\( \Rightarrow \frac{1}{{\frac{{125}}{3}}} + \frac{1}{{125}} = \frac{{2{Z_L}}}{{2500}} \Rightarrow {Z_L} = 40{\mkern 1mu} {\mkern 1mu} \left( \Omega \right)\)
\( \Rightarrow R = \sqrt {2500 - {{40}^2}} = 30{\mkern 1mu} {\mkern 1mu} \left( \Omega \right)\).
Đáp án: \(30\Omega \)
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số Biết rằng đồ thị hàm số đã cho đi qua điểm \(\left( { - 1\,;\,\,7} \right)\) và giao điểm hai đường tiệm cận là \(\left( { - 2\,;\,\,3} \right).\) Giá trị của biểu thức \(\frac{{2a + 3b + 4c + d}}{{7c}}\) bằng\(f\left( x \right) = \frac{{ax + b}}{{cx + d}}\,\,\left( {a,\,\,b,\,\,c,\,\,d \in \mathbb{R},\,\,c \ne 0} \right).\)
Xem đáp án »
26/06/2024
4,668
Câu 2:
Có bao nhiêu giá trị nguyên của tham số \[m \in \left[ { - 10\,;\,\,10} \right]\] để đồ thị hàm số \(y = \frac{{x - 1}}{{2{x^2} + 6x - m - 3}}\) có hai đường tiệm cận đứng?
Có bao nhiêu giá trị nguyên của tham số \[m \in \left[ { - 10\,;\,\,10} \right]\] để đồ thị hàm số \(y = \frac{{x - 1}}{{2{x^2} + 6x - m - 3}}\) có hai đường tiệm cận đứng?
Xem đáp án »
13/07/2024
4,115
Câu 3:
Trong không gian \[Oxyz,\] cho bốn điểm \[A\left( {1\,;\,\, - 2\,;\,\,0} \right),\,\,B\left( {2\,;\,\,0\,;\,\,3} \right),\]\[C\left( { - 2\,;\,\,1\,;\,\,3} \right),\]\[D\left( {0\,;\,\,1\,;\,\,1} \right)\]. Thể tích khối tứ diện \[ABCD\] bằng
Trong không gian \[Oxyz,\] cho bốn điểm \[A\left( {1\,;\,\, - 2\,;\,\,0} \right),\,\,B\left( {2\,;\,\,0\,;\,\,3} \right),\]\[C\left( { - 2\,;\,\,1\,;\,\,3} \right),\]\[D\left( {0\,;\,\,1\,;\,\,1} \right)\]. Thể tích khối tứ diện \[ABCD\] bằng
Xem đáp án »
26/06/2024
3,570
Câu 4:
Có bao nhiêu giá trị nguyên của tham số \(m \in \left[ { - 20\,;\,\,20} \right]\) để hàm số \(y = - {x^4} + 6{x^2} + \left( {m - 2} \right)x + 3\) có đúng một điểm cực trị?
Có bao nhiêu giá trị nguyên của tham số \(m \in \left[ { - 20\,;\,\,20} \right]\) để hàm số \(y = - {x^4} + 6{x^2} + \left( {m - 2} \right)x + 3\) có đúng một điểm cực trị?
Xem đáp án »
26/06/2024
1,870
Câu 5:
Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = \frac{m}{3}{x^3} - 2m{x^2} + \left( {3m + 5} \right)x\) đồng biến trên \(\mathbb{R}\)?
Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = \frac{m}{3}{x^3} - 2m{x^2} + \left( {3m + 5} \right)x\) đồng biến trên \(\mathbb{R}\)?
Xem đáp án »
26/06/2024
1,764
Câu 6:
Trong không gian \[Oxyz,\] phương trình mặt cầu đi qua điểm \[A\left( {1\,;\,\, - 1\,;\,\,4} \right)\] và tiếp xúc với các mặt phẳng tọa độ là
Xem đáp án »
26/06/2024
1,019
Câu 7:
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \frac{1}{{x - 1}} + 6x\,,\,\,\forall x \in \left( {1\,;\,\, + \infty } \right)\) và \(f(2) = 12.\) Biết \(F\left( x \right)\) là nguyên hàm của \(f\left( x \right)\) thỏa mãn \(F(2) = 6\), khi đó giá trị biểu thức \(F\left( 5 \right) - 4F\left( 3 \right)\) bằng
Xem đáp án »
26/06/2024
853
về câu hỏi!