Hiện tại, mỗi tháng một cửa hàng đồ lưu niệm bán được 100 sản phẩm A. Với mỗi sản phẩm A bán được, cửa hàng thu được 20 nghìn đồng lợi nhuận. Qua khảo sát, người ta thấy rằng với mỗi nghìn đồng giảm giá, cửa hàng bán thêm được 10 sản phẩm A. Cửa hàng nên giảm giá bao nhiêu cho mỗi sản phẩm A để thu được lợi nhuận lớn nhất từ việc bán sản phẩm này? Tính lợi nhuận lớn nhất đó.
Quảng cáo
Trả lời:
Gọi x (nghìn đồng, x ≥ 0) là số tiền giảm giá cho mỗi sản phẩm A.
Với mỗi nghìn đồng giảm giá, cửa hàng bán thêm được 10 sản phẩm A nên với x nghìn đồng giảm giá, cửa hàng bán thêm được 10x sản phẩm A. Khi đó, mỗi tháng cửa hàng bán được số sản phẩm là 100 + 10x (sản phẩm).
Khi giảm giá x nghìn đồng cho mỗi sản phẩm A thì lợi nhuận trên mỗi sản phẩm A bán ra được lúc này là 20 – x (nghìn đồng).
Rõ ràng 20 – x ≥ 0, do đó x phải thỏa mãn điều kiện 0 ≤ x ≤ 20.
Lợi nhuận từ việc bán sản phẩm A của cửa hàng trong một tháng sau khi giảm giá là
L(x) = (100 + 10x) ∙ (20 – x) = 2 000 + 100x – 10x2 (nghìn đồng).
Xét hàm số L(x) = 2 000 + 100x – 10x2 với x ∈ [0; 20].
Ta có L'(x) = 100 – 20x;
L'(x) = 0 ⇔ 100 – 20x = 0 ⇔ x = 5 ∈ [0; 20].
Ta có L(0) = 2 000; L(5) = 2 250; L(20) = 0.
Suy ra ![]() , đạt được tại x = 5.
, đạt được tại x = 5.
Vậy cửa hàng nên giảm giá 5 nghìn đồng cho mỗi sản phẩm A để thu được lợi nhuận lớn nhất từ việc bán sản phẩm này là 2 triệu 250 nghìn đồng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
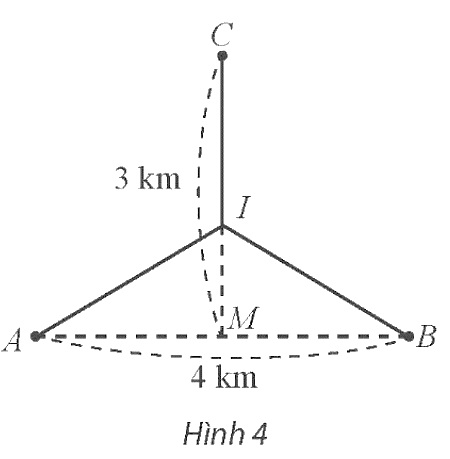
Đặt IM = x (km, 0 ≤ x ≤ 3).
Suy ra IC = 3 – x (km).
Vì M là trung điểm của AB nên MA = MB = 2 km.
Áp dụng định lí Pythagore trong các tam giác vuông AMI và BMI, ta có:
IA = IB = ![]() (km).
(km).
Tổng độ dài đường ống dẫn nước thải là
d = IA + IB + IC = ![]() (km).
(km).
Xét hàm số y = ![]() với 0 ≤ x ≤ 3, ta có:
với 0 ≤ x ≤ 3, ta có:
y' = 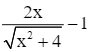 ;
;
y' = 0 ⇔ 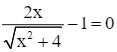
![]()
⇔ 3x2 = 4 ⇒ x = 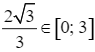 .
.
Ta có y(0) = 7; 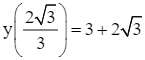 ; y(3) =
; y(3) = ![]() .
.
Do đó, 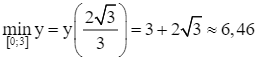 .
.
Suy ra giá trị nhỏ nhất của d khoảng 6,46 km, đạt được khi 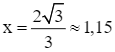 (km).
(km).
Vậy cần chọn vị trí điểm I đặt cách vị trí M (trung điểm của AB) một khoảng xấp xỉ bằng 1,15 km thì tổng độ dài đường ống dẫn nước thải nhỏ nhất và giá trị nhỏ nhất này xấp xỉ bằng 6,46 km.
Lời giải
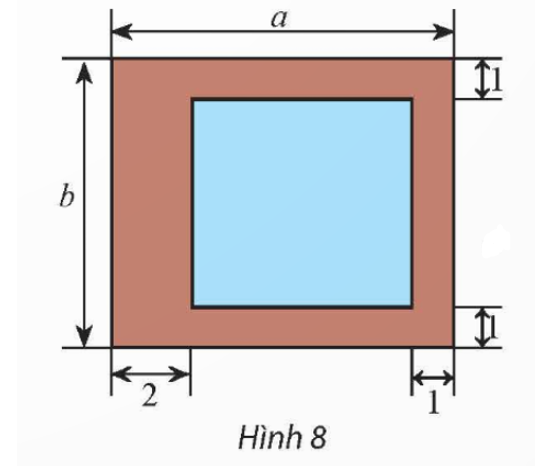
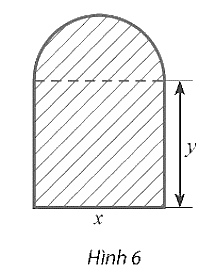
Từ hình vẽ, ta tính được kích thước hình chữ nhật phần mặt nước là a – 3 (m) và b – 2 (m). Từ đó suy ra a > 3 và b > 2.
Diện tích phần mặt nước là S1 = (a – 3)(b – 2) = 54 (m2)
Suy ra 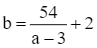 (m).
(m).
Diện tích phần đường đi là S = ab – 54 = 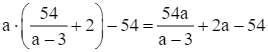 (m2).
(m2).
Xét hàm số 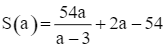 với a ∈ (3; + ∞).
với a ∈ (3; + ∞).
Ta có 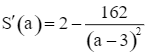 ;
;
S'(a) = 0 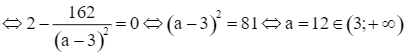 .
.
Bảng biến thiên:
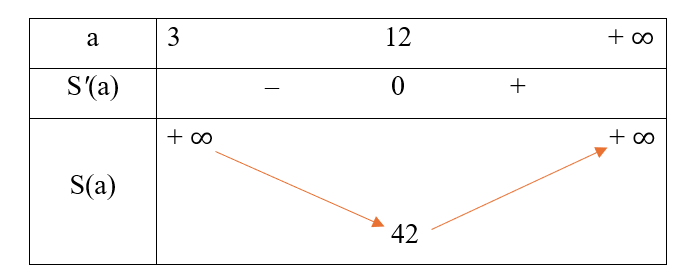
Từ bảng biến thiên, ta có ![]() , đạt được khi a = 12.
, đạt được khi a = 12.
Với a = 12 thì ta có 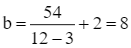 .
.
Vậy bề mặt của lồng có chiều dài và chiều rộng lần lượt là 12 m và 8 m thì diện tích phần đường đi là bé nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.