Giải chuyên đề Toán 12 CTST Bài 2. Vận dụng đạo hàm giải bài toán tối ưu có đáp án
49 người thi tuần này 4.6 1.1 K lượt thi 17 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề cương ôn tập cuối kì 2 Toán 12 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Chương IV. Nguyên hàm và tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Tự luận
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 1. Phương trình mặt phẳng
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 4. Ứng dụng hình học của tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 3. Tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 2. Nguyên hàm của một số hàm số sơ cấp
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 1. Nguyên hàm
Đề cương ôn tập giữa kì 2 Toán 12 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Tự luận
Danh sách câu hỏi:
Lời giải
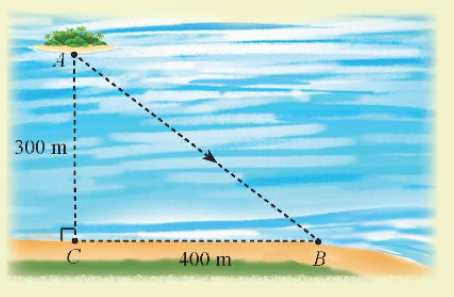
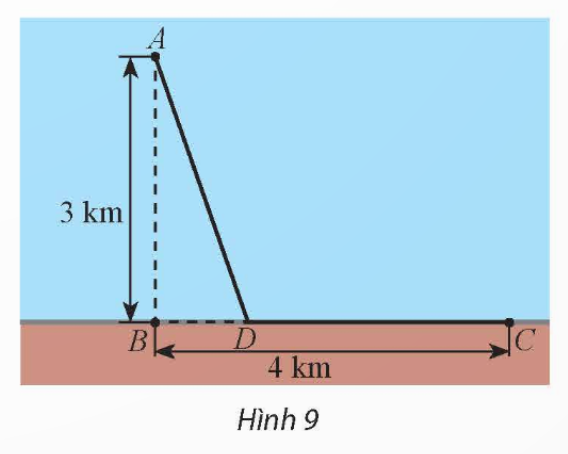
Sau bài học này, ta giải quyết được bài toán trên như sau:
Áp dụng định lý Pythagore, ta tính được AB = 500 m.
Do đó, nếu người đó chèo thuyền thẳng từ A đến B thì tốn 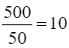 phút.
phút.
Ta xem xét phương án sau:
Giả sử người đó chèo thuyền thẳng đến điểm D nằm giữa B và C và cách C một đoạn x (m), rồi chạy bộ thẳng đến B.
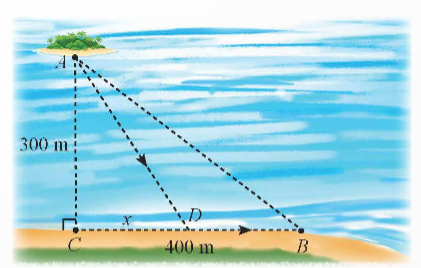
Ta cần tìm giá trị của x để người đó tốn ít thời gian nhất.
Ta có: ![]() (m); DB = 400 – x (m) với 0 ≤ x ≤ 400.
(m); DB = 400 – x (m) với 0 ≤ x ≤ 400.
Thời gian người đó tiêu tốn là
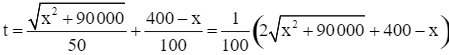 (phút).
(phút).
Xét hàm số ![]() với 0 ≤ x ≤ 400, ta có:
với 0 ≤ x ≤ 400, ta có:
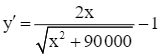 ;
;
y' = 0 ⇔ 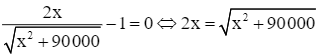 ⇔ 4x2 = x2 + 90 000
⇔ 4x2 = x2 + 90 000
⇔ x2 = 30 000 ⇔ x = ![]() ∈ [0; 400].
∈ [0; 400].
Ta có y(0) = 1 000; ![]() ; y(400) = 1 000.
; y(400) = 1 000.
Vậy ![]() .
.
Suy ra giá trị nhỏ nhất của t là 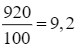 (phút), đạt được khi x =
(phút), đạt được khi x = ![]() ≈ 173 (m).
≈ 173 (m).
Do đó, người đó tốn ít thời gian nhất khi x = ![]() ≈ 173 (m).
≈ 173 (m).
Nhận thấy 9,2 phút < 10 phút nên người đó chèo thuyền từ A thẳng đến điểm D nằm giữa B và C và cách C một đoạn xấp xỉ bằng 173 m, rồi chạy bộ thẳng đến B là phương án tốn ít thời gian nhất.
Lời giải
Lời giải
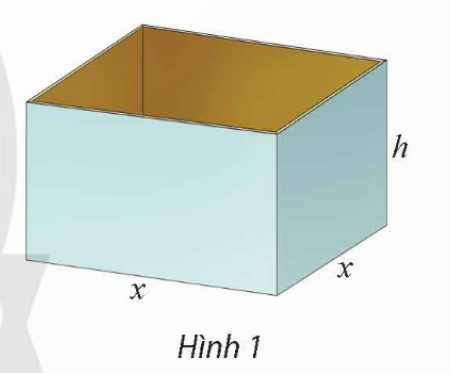
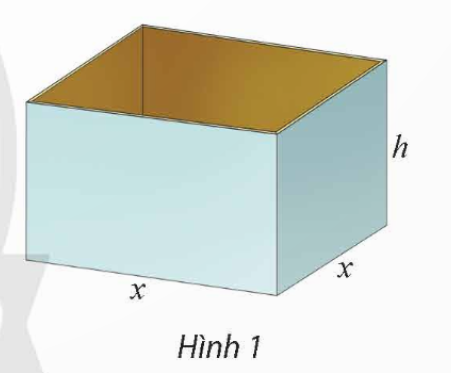
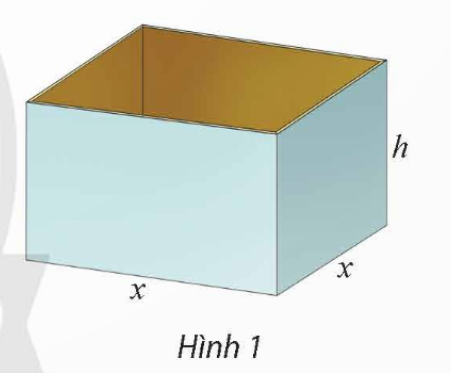
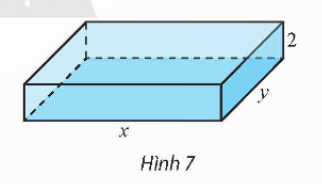
Thể tích của thùng là V = x2h = 500 (dm3).
Suy ra 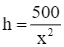 (dm).
(dm).
Vì 3 ≤ h ≤ 10 nên 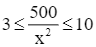 , suy ra
, suy ra 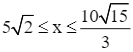 .
.
Khi đó, tổng diện tích các mặt của thùng là
S(x) = 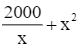 (dm2) với
(dm2) với 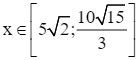 .
.
Lời giải
Xét hàm số S(x) = 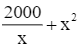 (dm2) với
(dm2) với 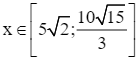 .
.
Ta có S'(x) = 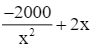 ;
;
Trên khoảng 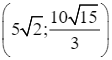 , S'(x) = 0 ⇔ x = 10.
, S'(x) = 0 ⇔ x = 10.
Có ![]() ; S(10) = 300;
; S(10) = 300; 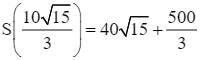 .
.
Do đó, 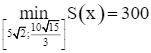 tại x = 10.
tại x = 10.
Vậy với x = 10 dm thì S có giá trị nhỏ nhất.
Lời giải
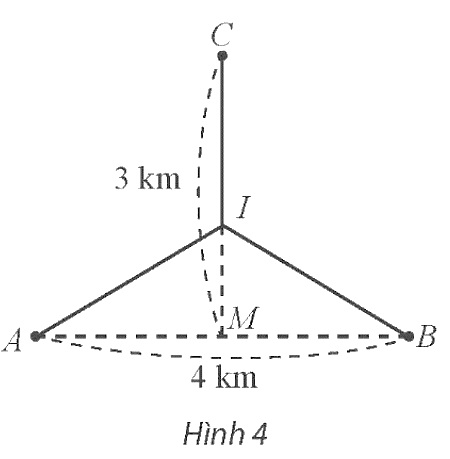
Đặt IM = x (km, 0 ≤ x ≤ 3).
Suy ra IC = 3 – x (km).
Vì M là trung điểm của AB nên MA = MB = 2 km.
Áp dụng định lí Pythagore trong các tam giác vuông AMI và BMI, ta có:
IA = IB = ![]() (km).
(km).
Tổng độ dài đường ống dẫn nước thải là
d = IA + IB + IC = ![]() (km).
(km).
Xét hàm số y = ![]() với 0 ≤ x ≤ 3, ta có:
với 0 ≤ x ≤ 3, ta có:
y' = 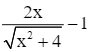 ;
;
y' = 0 ⇔ 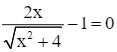
![]()
⇔ 3x2 = 4 ⇒ x = 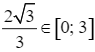 .
.
Ta có y(0) = 7; 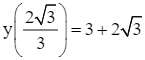 ; y(3) =
; y(3) = ![]() .
.
Do đó, 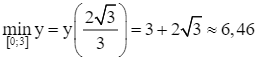 .
.
Suy ra giá trị nhỏ nhất của d khoảng 6,46 km, đạt được khi 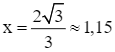 (km).
(km).
Vậy cần chọn vị trí điểm I đặt cách vị trí M (trung điểm của AB) một khoảng xấp xỉ bằng 1,15 km thì tổng độ dài đường ống dẫn nước thải nhỏ nhất và giá trị nhỏ nhất này xấp xỉ bằng 6,46 km.
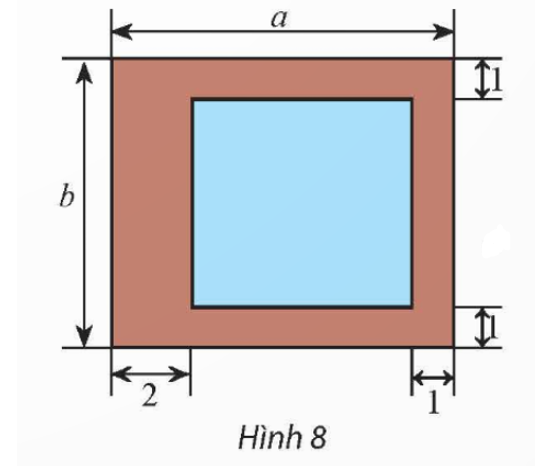
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.