Giải SBT Toán 12 Chân trời sáng tạo Bài 1. Vectơ và các phép toán trong không gian có đáp án
25 người thi tuần này 4.6 812 lượt thi 9 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề cương ôn tập cuối kì 2 Toán 12 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Chương IV. Nguyên hàm và tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Tự luận
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 1. Phương trình mặt phẳng
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 4. Ứng dụng hình học của tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 3. Tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 2. Nguyên hàm của một số hàm số sơ cấp
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 1. Nguyên hàm
Đề cương ôn tập giữa kì 2 Toán 12 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Tự luận
Danh sách câu hỏi:
Lời giải
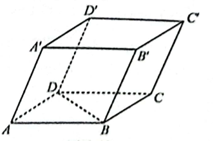
a) Các vectơ có điểm đầu là B và điểm cuối là các đỉnh của hình hộp không cùng nằm trên một mặt của hình hộp với điểm B là: \(\overrightarrow {BD'} \).
b) Các vectơ bằng vectơ \(\overrightarrow {BC} \) là \(\overrightarrow {AD} ,\overrightarrow {A'D'} ,\overrightarrow {B'C'} \).
c) Các vectơ đối của vectơ \(\overrightarrow {BD} \) là \(\overrightarrow {DB} ,\overrightarrow {D'B'} \).
Lời giải
a) Ta có: \(\overrightarrow {OA} + \overrightarrow {AB} - \overrightarrow {OC} \) = \(\overrightarrow {OB} - \overrightarrow {OC} = \overrightarrow {CB} \).
b) Dựng hình hộp OADB.CFEK
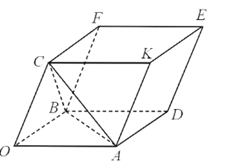
Ta có: \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} \) = \(\overrightarrow {OD} + \overrightarrow {OC} = \overrightarrow {OE} \).
Lời giải
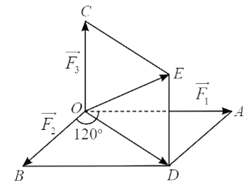
Gọi \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) lần lượt là ba lực tác động vào một vật đặt tại điểm O như Hình 2.
Ta có: \(\overrightarrow {{F_1}} = \overrightarrow {OA} \), \(\overrightarrow {{F_2}} = \overrightarrow {OB} \), \(\overrightarrow {{F_3}} = \overrightarrow {OC} \).
Độ lớn các lực: F1 = OA = 10 N, F2 = OB = 8 N, F3 = OC = 6 N.
Dựng hình bình hành OADB. Theo quy tắc hình bình hành, ta có: \(\overrightarrow {OD} = \overrightarrow {OA} + \overrightarrow {OB} \).
Suy ra \({\overrightarrow {OD} ^2} = {\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)^2} = {\overrightarrow {OA} ^2} + {\overrightarrow {OB} ^2} + 2\overrightarrow {OA} .\overrightarrow {OB} \)
Mà \(\overrightarrow {OA} .\overrightarrow {OB} \) = OA.OB.cos\(\left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right)\)
⇒ OD2 = OA2 + OB2 + 2OA.OB.cos120°.
Dựng hình bình hành ODEC.
Tổng lực tác động vào vật là \(\overrightarrow F = \overrightarrow {OE} = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} \).
Độ lớn của hợp lực tác động vào vật là F = OE.
Vì \(OC \bot \left( {OADB} \right)\) nên OC ⊥ OD, suy ra ODEC là hình chữ nhật.
Do đó, tam giác ODE vuông tại D.
Khi đó, OE2 = OC2 + OD2 = OC2 + OA2 + OB2 + 2OA.OB.cos120°.
Suy ra OE = \(\sqrt {O{C^2} + O{A^2} + O{B^2} + 2.OA.OB\cos 120^\circ } \)
= \(\sqrt {{6^2} + {{10}^2} + {8^2} + 2.10.8.\cos 120^\circ } \) ≈ 10,95.
Do đó, F = OE ≈ 10,95 N.
Lời giải
a) Theo quy tắc hình hộp, ta có: \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \) = \(\overrightarrow {AC'} \).
Suy ra \(\left| {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right| = \left| {\overrightarrow {AC'} } \right|\) = AC' = 2AO = 2a.
b) Ta có: \(\overrightarrow {C'B'} + \overrightarrow {C'D'} + \overrightarrow {A'A} \) = \(\overrightarrow {C'B'} + \overrightarrow {C'D'} + \overrightarrow {C'C} = \overrightarrow {C'A} \)
Suy ra \(\left| {\overrightarrow {C'B'} + \overrightarrow {C'D'} + \overrightarrow {A'A} } \right| = \left| {\overrightarrow {C'A} } \right| = C'A = 2a\).
Lời giải
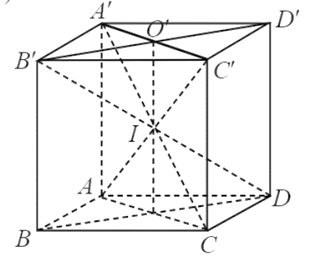
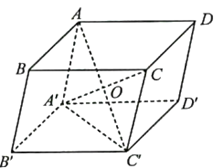
a) Ta có: \(\overrightarrow {OA'} + \overrightarrow {OB'} + \overrightarrow {OC'} + \overrightarrow {OD'} \) = \(\left( {\overrightarrow {OA'} + \overrightarrow {OC'} } \right) + \left( {\overrightarrow {OB'} + \overrightarrow {OD'} } \right)\) = \(2\overrightarrow {OO'} + 2\overrightarrow {OO'} \) = \(4\overrightarrow {OO'} \).
b) Ta có bốn đường chéo của hình lập phương cắt nhau tại trung điểm I của mỗi đường chéo nên I cũng là trung điểm của DB'. Suy ra \(\overrightarrow {DB} + \overrightarrow {DD'} = \overrightarrow {DB'} = 2\overrightarrow {DI} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.