Giải SGK Toán 12 CTST Bài 3. Ứng dụng hình học của tích phân có đáp án

33 người thi tuần này 4.6 822 lượt thi 21 câu hỏi

Câu 1

Ta đã biết công thức tính thể tích của khối cầu bán kính R là $V = \frac{4 π R^{3}}{3}$ . Làm thế nào để tìm ra công thức đó?

Xem đáp án

Lời giải

Sau khi học xong bài, ta giải quyết bài toán này như sau:

Ta đã biết công thức tính thể tích của khối cầu bán kính R là V = 4pi R^3/ 3 . Làm thế nào để tìm ra công thức đó? (ảnh 1)

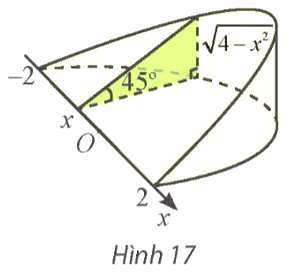
Khối cầu có bán kính R là khối tròn xoay nhận được khi quay nửa hình tròn giới hạn bởi đồ thị hàm số $y = \sqrt {{R^2} - {x^2}} \left( { - R \le x \le R} \right)$ và trục Ox quanh trục Ox.

Từ đó thể tích khối cầu là:

$V = \pi \int\limits_{ - R}^R {\left( {{R^2} - {x^2}} \right)dx} = \left. {\pi \left( {{R^2}x - \frac{{{x^3}}}{3}} \right)} \right|_{ - R}^R = \frac{{4\pi {R^3}}}{3}$.

Câu 2

Gọi d là đồ thị của hàm số y = f(x) = 6 – 2x. Kí hiệu S₁ là diện tích hình phẳng giới hạn bởi d, trục hoành và trục tung, S₂ là diện tích hình phẳng giới hạn bởi d, trục hoành và đường thẳng x = 5 (Hình 1).

a) Tính S₁ và so sánh với $\int\limits_0^3 {f\left( x \right)dx} $.

b) Tính S₂ và so sánh với $\int\limits_3^5 {f\left( x \right)dx} $.

c) So sánh $\int\limits_0^5 {\left| {f\left( x \right)} \right|dx} $ với S₁ + S₂.

Xem đáp án

Lời giải

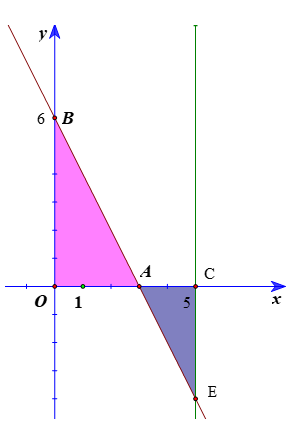
Gọi d là đồ thị của hàm số y = f(x) = 6 – 2x. Kí hiệu S1 là diện tích hình phẳng giới hạn bởi d, trục hoành (ảnh 2)

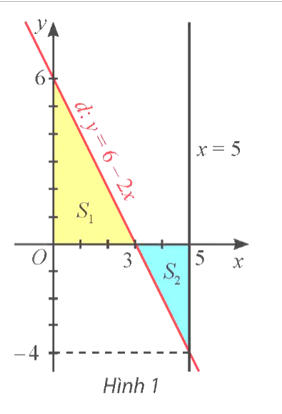
a) Gọi A(3; 0), B(0; 6), C(5; 0), E(5; −4).

Ta có S₁ chính là diện tích của tam giác vuông OAB với OA = 3, OB = 6.

Do đó ${S_1} = {S_{\Delta OAB}} = \frac{1}{2}OA.OB = \frac{1}{2}.3.6 = 9$.

Ta có $\int\limits_0^3 {f\left( x \right)dx} $$ = \int\limits_0^3 {\left( {6 - 2x} \right)dx} $\[ = \left. {\left( {6x - {x^2}} \right)} \right|_0^3\] = 9.

Vậy ${S_1} = \int\limits_0^3 {f\left( x \right)dx} $.

b) Ta có S₂ chính là diện tích của tam giác vuông ACE với AC = 2, CE = 4.

Do đó ${S_2} = {S_{\Delta ACE}} = \frac{1}{2}AC.CE = \frac{1}{2}.2.4 = 4$.

Ta có $\int\limits_3^5 {f\left( x \right)dx} $$ = \int\limits_3^5 {\left( {6 - 2x} \right)dx} $\[ = \left. {\left( {6x - {x^2}} \right)} \right|_3^5\] = 5 – 9 = −4.

Do đó ${S_2} = - \int\limits_3^5 {f\left( x \right)dx} $.

c) Ta có $\int\limits_0^5 {\left| {f\left( x \right)} \right|dx} $= $\int\limits_0^5 {\left| {6 - 2x} \right|dx} $$ = \int\limits_0^3 {\left| {6 - 2x} \right|dx} + \int\limits_3^5 {\left| {6 - 2x} \right|dx} $

$ = \int\limits_0^3 {\left( {6 - 2x} \right)dx} + \int\limits_3^5 {\left( {2x - 6} \right)dx} $$ = \left. {\left. {\left( {6x - {x^2}} \right)} \right|_0^3 + \left( {{x^2} - 6x} \right)} \right|_3^5$

= 9 − 5 + 9 = 13.

Có S₁ + S₂ = 9 + 4 = 13 = $\int\limits_0^5 {\left| {f\left( x \right)} \right|dx} $.

Câu 3

Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số y = 2x – x², trục hoành và hai đường thẳng x = 0, x = 3.

Xem đáp án

Lời giải

Ta có 2x – x² = 0 Û x = 0 hoặc x = 2.

Với x Î [0; 2] thì 2x – x² ≥ 0, với x Î [2; 3] thì 2x – x² ≤ 0.

Diện tích cần tính là:

$S = \int\limits_0^3 {\left| {2x - {x^2}} \right|dx} $$ = \int\limits_0^2 {\left| {2x - {x^2}} \right|dx} + \int\limits_2^3 {\left| {2x - {x^2}} \right|dx} $$ = \int\limits_0^2 {\left( {2x - {x^2}} \right)dx} + \int\limits_2^3 {\left( {{x^2} - 2x} \right)dx} $

$ = \left. {\left( {{x^2} - \frac{{{x^3}}}{3}} \right)} \right|_0^2 + \left. {\left( {\frac{{{x^3}}}{3} - {x^2}} \right)} \right|_2^3$$ = \frac{4}{3} + \frac{4}{3} = \frac{8}{3}$.

Câu 4

Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số y = cosx – 2, trục hoành và hai đường thẳng x = 0, x = π.

Xem đáp án

Lời giải

Với x Î [0; π] thì −1 ≤ cosx ≤ 1 nên −3 ≤ cosx − 2 ≤ −1 Þ cosx − 2 < 0.

Diện tích cần tính là:

$S = \int\limits_0^\pi {\left| {\cos x - 2} \right|} dx$$ = \int\limits_0^\pi {\left( {2 - \cos x} \right)} dx$$ = \left. {\left( {2x - \sin x} \right)} \right|_0^\pi $= 2π.

Câu 5

Cho hai hàm số y = 4x – x² và y = x lần lượt có đồ thị (P) và d như Hình 4.

a) Tính diện tích S₁ của hình phẳng giới hạn bởi (P), trục hoành và hai đường thẳng x = 0, x = 2.

b) Tính diện tích S của hình phẳng giới hạn bởi (P), d và hai đường thẳng x = 0, x = 2.

Xem đáp án

Lời giải

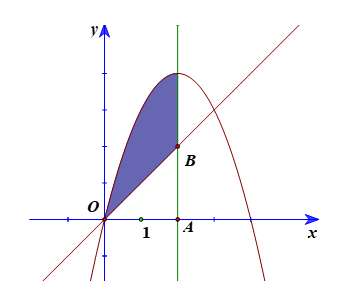
Cho hai hàm số y = 4x – x^2 và y = x lần lượt có đồ thị (P) và d như Hình 4. (ảnh 2)

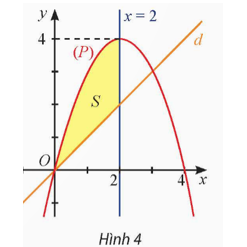
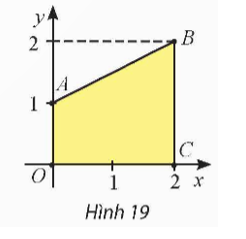
a) Ta có ${S_1} = \int\limits_0^2 {\left| {4x - {x^2}} \right|dx} $$ = \int\limits_0^2 {\left( {4x - {x^2}} \right)dx} $$ = \left. {\left( {2{x^2} - \frac{{{x^3}}}{3}} \right)} \right|_0^2$$ = \frac{{16}}{3}$.

b) Gọi A(2; 0), B(2; 2).

Ta có tam giác OAB là tam giác vuông tại A, có OA = 2, AB = 2.

Suy ra ${S_{\Delta OAB}} = \frac{1}{2}.OA.AB = \frac{1}{2}.2.2 = 2$.

Do đó $S = {S_1} - {S_{\Delta OAB}} = \frac{{16}}{3} - 2 = \frac{{10}}{3}$.

Câu 6

Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số y = x² – 2x – 1, y = x – 1 và hai đường thẳng x = 1, x = 4.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Tiếng Anh

Giáo dục Kinh tế và Pháp luật

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Tin học

Giáo dục Kinh tế và Pháp luật

Global success

iLearn Smart World

Friends Global

Explore new worlds

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử