Câu hỏi:
13/07/2024 21,548
Trong mặt phẳng tọa độ Oxy, cho hình thang OABC có A(0; 1), B(2; 2) và C(2; 0) (Hình 19). Tính thể tích khối tròn xoay tạo thành khi quay hình thang OABC quanh trục Ox.
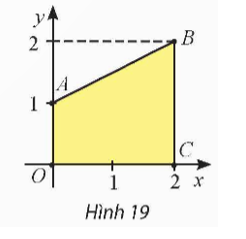
Trong mặt phẳng tọa độ Oxy, cho hình thang OABC có A(0; 1), B(2; 2) và C(2; 0) (Hình 19). Tính thể tích khối tròn xoay tạo thành khi quay hình thang OABC quanh trục Ox.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có OABC là hình thang vuông, có đường cao OC nằm trên trục Ox.
Khi quay hình thang OABC quanh trục Ox ta được khối tròn xoay là khối nón cụt, có bán kính đáy bé r1 = OA = 1, bán kính đáy lớn r2 = BC = 2 và chiều cao h = OC = 2.
Thể tích cần tính là:
\(V = \frac{1}{3}\pi \left( {r_1^2 + {r_1}{r_2} + r_2^2} \right)h = \frac{1}{3}\pi \left( {{1^2} + 1.2 + {2^2}} \right).2 = \frac{{14\pi }}{3}\).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
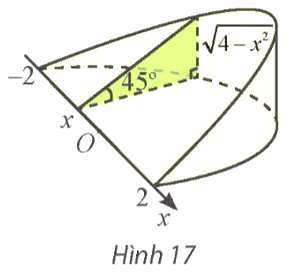
Vì mặt cắt là tam giác vuông có một góc 45° nên mặt cắt là tam giác vuông cân.
Do đó diện tích của mặt cắt là \(S\left( x \right) = \frac{1}{2}{\left( {\sqrt {4 - {x^2}} } \right)^2} = \frac{1}{2}\left( {4 - {x^2}} \right) = 2 - \frac{1}{2}{x^2}\).
Thể tích vật thể là:
\(V = \int\limits_{ - 2}^2 {\left( {2 - \frac{1}{2}{x^2}} \right)dx} \)\( = \left. {\left( {2x - \frac{{{x^3}}}{6}} \right)} \right|_{ - 2}^2\)\( = \frac{8}{3} + \frac{8}{3} = \frac{{16}}{3}\).
Lời giải
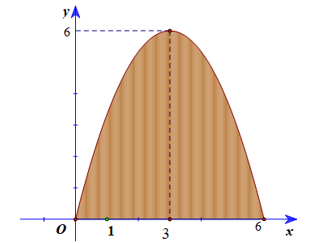
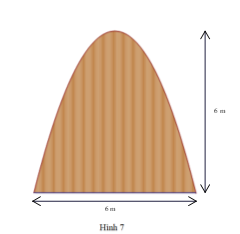
Chon hệ tọa độ Oxy như hình vẽ.
Giả sử (P): y = ax2 + bx + c (a ≠ 0).
Vì (P) đi qua các điểm (0; 0), (6; 0), (3; 6) nên ta có:
\(\left\{ \begin{array}{l}c = 0\\36a + 6b = 0\\9a + 3b = 6\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = - \frac{2}{3}\\b = 4\\c = 0\end{array} \right.\).
Vậy (P): \(y = - \frac{2}{3}{x^2} + 4x\).
Bài toán trở thành tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = - \frac{2}{3}{x^2} + 4x\), trục hoành và hai đường thẳng x = 0, x = 6.
Diện tích cần tính là:
\(S = \int\limits_0^6 {\left| { - \frac{2}{3}{x^2} + 4x} \right|} dx\)\( = \int\limits_0^6 {\left( { - \frac{2}{3}{x^2} + 4x} \right)} dx\)\( = \left. {\left( { - \frac{{2{x^3}}}{9} + 2{x^2}} \right)} \right|_0^6 = 24\) m2.
Vậy diện tích của cửa hầm là 24 m2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo