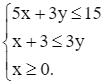Quảng cáo
Trả lời:
Viết lại ràng buộc của bài toán thành
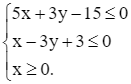
Tập phương án Ω của bài toán là miền tam giác ABC được tô màu như hình vẽ dưới đây.
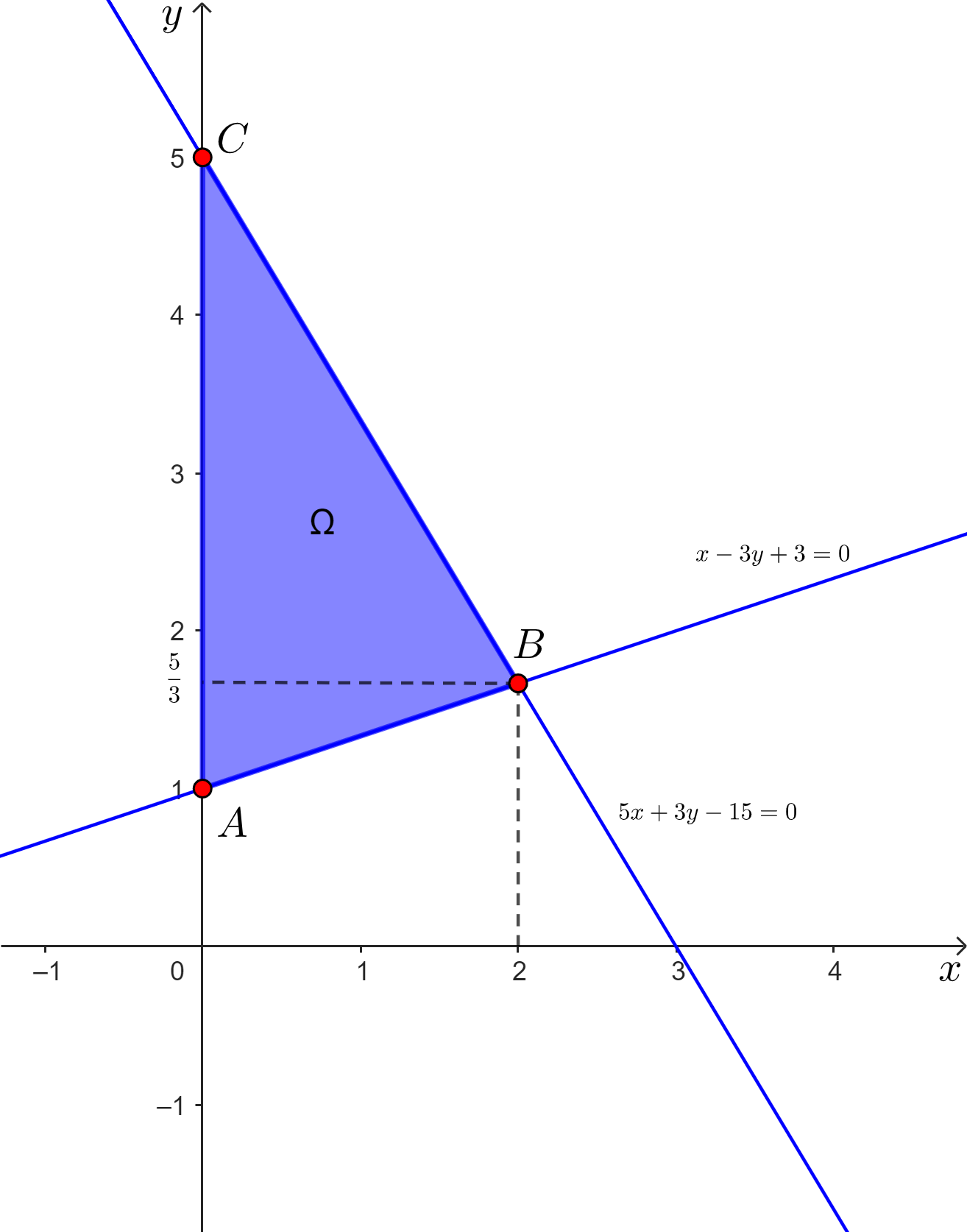
Tọa độ giao điểm A của hai đường thẳng x = 0 và x – 3y + 3 = 0 là nghiệm của hệ phương trình 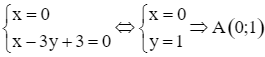 .
.
Tương tự, ta tìm được 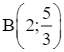 và C(0; 5).
và C(0; 5).
Giá trị của biểu thức F tại các đỉnh của Ω:
F(0; 1) = 40 ∙ 0 + 15 ∙ 1 = 15;
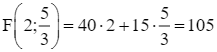 ;
;
F(0; 5) = 40 ∙ 0 + 15 ∙ 5 = 75.
Từ đó, 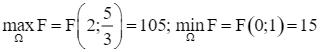 .
.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: B
Gọi x, y (x ≥ 0; y ≥ 0; x, y ∈ ℤ) lần lượt là số chiếc xe tại loại A và loại B nhà phân phối thuê để vận chuyển máy giặt.
Vì có thể thuê tối đa 3 chiếc xe tải loại A và 8 chiếc xe tải loại B nên x ≤ 3 và y ≤ 8.
Tổng số máy giặt vận chuyển nhiều nhất được khi dùng x xe loại A và y xe loại B nếu mỗi xe chỉ chở nhiều nhất một chuyến là 20x + 10y (chiếc).
Vì phải vận chuyển 100 chiếc máy giặt nên 20x + 10y ≥ 100 hay 2x + y ≥ 10.
Số tiền cước (triệu đồng) mà nhà phân phối phải trả là F = 3x + 2y.
Từ đó, ta nhận được bài toán quy hoạch tuyến tính:
F = 3x + 2y → min
với ràng buộc
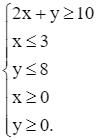
Tập phương án Ω của bài toán là miền tam giác ABC được tô màu như hình vẽ dưới và có các đỉnh là A(1; 8), B(3; 8) và C(3; 4).
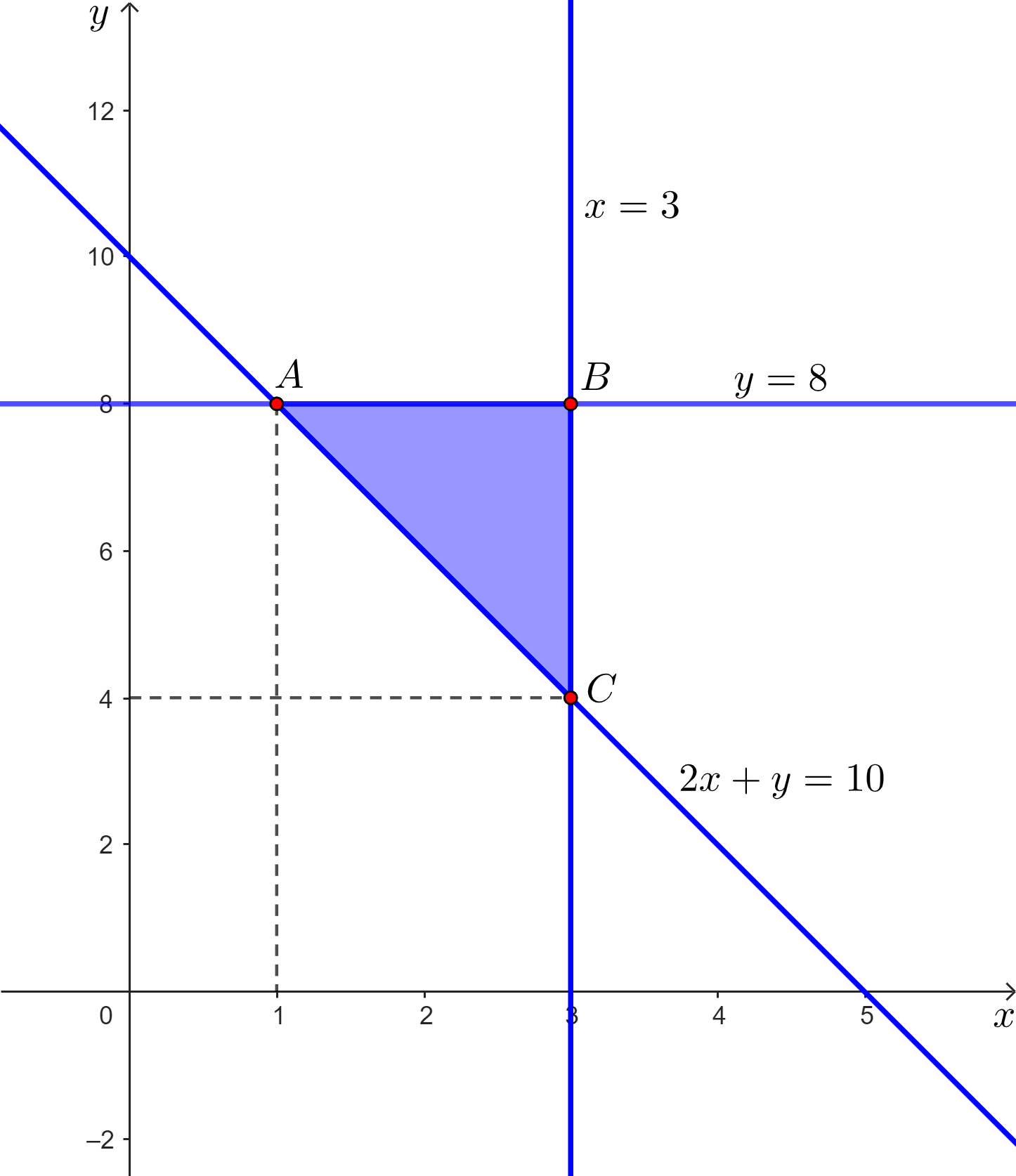
Giá trị của F tại các đỉnh:
F(1; 8) = 3 ∙ 1 + 2 ∙ 8 = 19;
F(3; 8) = 3 ∙ 3 + 2 ∙ 8 = 25;
F(3; 4) = 3 ∙ 3 + 2 ∙ 4 = 17.
Suy ra ![]() .
.
Vậy số tiền cước tối thiểu mà nhà phân phối phải trả là 17 triệu đồng.
Lời giải
Doanh thu của đơn vị tổ chức buổi biểu diễn văn nghệ là:
D = px = 500 ∙ e– 0,0005x ∙ x = 500xe– 0,0005x (nghìn đồng) với x > 0.
Xét hàm số f(x) = 500xe– 0,0005x với x ∈ (0; + ∞).
Ta có f'(x) = 500e– 0,0005x(1 – 0,0005x);
f'(x) = 0 ⇔ 1 – 0,0005x = 0 ⇔ x = 2 000 ∈ (0; + ∞).
Bảng biến thiên:
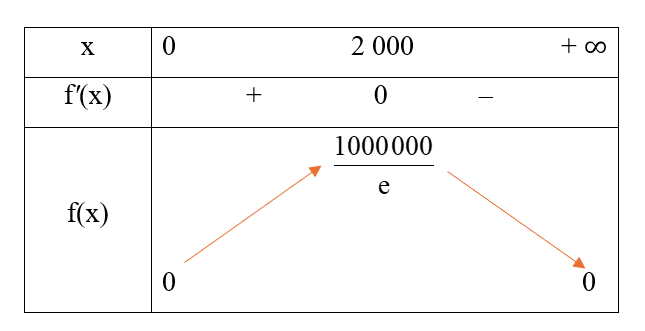
Từ bảng biến thiên, ta có 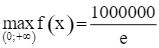 , đạt được khi x = 2 000.
, đạt được khi x = 2 000.
Với x = 2 000, ta có p = 500 ∙ e– 0,0005 ∙ 2 000 = ![]() ≈ 184.
≈ 184.
Vậy đơn vị tổ chức nên bán vé với giá 184 nghìn đồng thì đạt được doanh thu cao nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.