Câu hỏi:
12/07/2024 6,762
Phần mềm của máy tiện kĩ thuật số CNC (Computer Numerical Control) đang biểu diễn một chi tiết máy như Hình 2.
a) Tìm tọa độ các điểm A, B, C, D.
b) Viết phương trình mặt phẳng (ABC) và mặt phẳng (ACD).
c) Viết phương trình tham số của đường thẳng AC.
d) Cho biết đầu mũi tiện đang đặt tại điểm M(0; 60; 40). Tính khoảng cách từ M đến mặt phẳng (ABC).
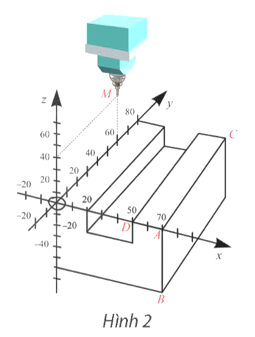
Phần mềm của máy tiện kĩ thuật số CNC (Computer Numerical Control) đang biểu diễn một chi tiết máy như Hình 2.
a) Tìm tọa độ các điểm A, B, C, D.
b) Viết phương trình mặt phẳng (ABC) và mặt phẳng (ACD).
c) Viết phương trình tham số của đường thẳng AC.
d) Cho biết đầu mũi tiện đang đặt tại điểm M(0; 60; 40). Tính khoảng cách từ M đến mặt phẳng (ABC).
Câu hỏi trong đề: Giải SGK Toán 12 CTST Bài tập cuối chương 5 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Ta có A(70; 0; 0), B(70; 0; −60), C(70; 80; 0), D(50; 0; 0).
b) Ta có \(\overrightarrow {AB} = \left( {0;0; - 60} \right),\overrightarrow {AC} = \left( {0;80;0} \right)\), \(\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {4800;0;0} \right)\).
Mặt phẳng (ABC) đi qua A(70; 0; 0), nhận \(\overrightarrow n = \frac{1}{{4800}}\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {1;0;0} \right)\) có phương trình là x – 70 = 0.
Có \(\overrightarrow {AC} = \left( {0;80;0} \right)\), \(\overrightarrow {AD} = \left( { - 20;0;0} \right)\), \(\left[ {\overrightarrow {AC} ,\overrightarrow {AD} } \right] = \left( {0;0;1600} \right)\).
Mặt phẳng (ACD) đi qua A(70; 0; 0), nhận \(\overrightarrow n = \frac{1}{{1600}}\left[ {\overrightarrow {AC} ,\overrightarrow {AD} } \right] = \left( {0;0;1} \right)\) có phương trình là z = 0.
c) Đường thẳng AC đi qua A(70; 0; 0) và nhận \(\overrightarrow a = \frac{1}{{80}}\overrightarrow {AC} = \left( {0;1;0} \right)\) có phương trình tham số là \(\left\{ \begin{array}{l}x = 70\\y = t\\z = 0\end{array} \right.\).
d) \(d\left( {M,\left( {ABC} \right)} \right) = \frac{{\left| {0 - 70} \right|}}{{\sqrt {{1^2}} }} = 70\).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
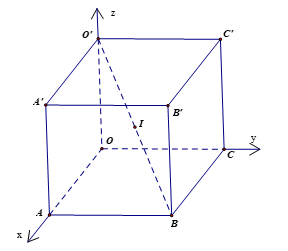
a) Mặt phẳng đoạn chắn của (O'AC) là \(\frac{x}{2} + \frac{y}{6} + \frac{z}{4} = 1\) Û 6x + 2y + 3z – 12 = 0.
b) Đường thẳng CO' đi qua C(0; 6; 0) nhận \(\frac{1}{2}\overrightarrow {CO'} = \left( {0; - 3;2} \right)\) làm vectơ chỉ phương có phương trình là \(\left\{ \begin{array}{l}x = 0\\y = 6 - 3t\\z = 2t\end{array} \right.\).
c) Mặt cầu đi qua các đỉnh của hình hộp có tâm I là trung điểm của O'B và bán kính IO'.
Có B(2; 6; 0), O'(0; 0; 4). Suy ra I(1; 3; 2) và \(IO' = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 3} \right)}^2} + {{\left( {4 - 2} \right)}^2}} = \sqrt {14} \).
Phương trình mặt cầu là: (x – 1)2 + (y – 3)2 + (z – 2)2 = 14.
Lời giải
a) Ta có \(\overrightarrow {BC} = \left( { - 1;2; - 7} \right),\overrightarrow {BD} = \left( {0;4; - 6} \right)\), \(\left[ {\overrightarrow {BC} ,\overrightarrow {BD} } \right] = \left( {16; - 6; - 4} \right)\)
Mặt phẳng (BCD) đi qua B(1; 0; 6) và nhận \(\overrightarrow n = \frac{1}{2}\left[ {\overrightarrow {BC} ,\overrightarrow {BD} } \right] = \left( {8; - 3; - 2} \right)\) có phương trình là 8(x – 1) – 3y – 2(z – 6) = 0 Û 8x – 3y – 2z + 4 = 0.
Thay tọa độ điểm A vào phương trình mặt phẳng (BCD) ta được:
8.(−2) – 3.6 – 2.3 + 4 = −36 ≠ 0.
Do đó A Ï (BCD). Suy ra ABCD là một tứ diện.
b) Ta có \(AH = d\left( {A,\left( {BCD} \right)} \right) = \frac{{\left| {8.\left( { - 2} \right) - 3.6 - 2.3 + 4} \right|}}{{\sqrt {{8^2} + {{\left( { - 3} \right)}^2} + {{\left( { - 2} \right)}^2}} }} = \frac{{36}}{{\sqrt {77} }}\).
c) Ta có \(\overrightarrow {AB} = \left( {3; - 6;3} \right)\) và \(\overrightarrow {CD} = \left( {1;2;1} \right)\), \(\left[ {\overrightarrow {AB} ,\overrightarrow {CD} } \right] = \left( { - 12;0;12} \right)\).
Mặt phẳng (α) đi qua A(−2; 6; 3) và nhận \(\overrightarrow n = - \frac{1}{{12}}\left[ {\overrightarrow {AB} ,\overrightarrow {CD} } \right] = \left( {1;0; - 1} \right)\) có phương trình là (x + 2) – (z – 3) = 0 Û x – z + 5 = 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận