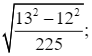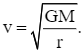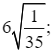Tốc độ v (m/s) của một tàu lượn siêu tốc di chuyển trên một cung tròn bán kính r (m) được cho bởi công thức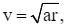 
trong đó a (m/s2) là gia tốc hướng tâm.
Nếu tàu lượn đang di chuyển với tốc độ 14 m/s và muốn đạt mức gia tốc hướng tâm tối đa là 7 m/s2 thì bán kính tối thiểu của cung tròn phải là bao nhiêu để tàu lượn không văng ra khỏi đường ray?
Tốc độ v (m/s) của một tàu lượn siêu tốc di chuyển trên một cung tròn bán kính r (m) được cho bởi công thức trong đó a (m/s2) là gia tốc hướng tâm.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Tàu lượn đang di chuyển với tốc độ 14 m/s nên v = 14 m/s.
Gia tốc hướng tâm tối đa là 7 m/s2 nên a ≤ 7 m/s2.
Từ biểu thức 
ta có 
Suy ra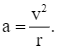 
Do đó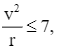 
suy ra 
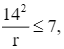do đó 196 ≤ 7r (do r > 0).
Suy ra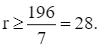 
Vậy bán kính tối thiểu của cung tròn để tàu lượn không văng ra khỏi đường ray là r = 28 m.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
⦁ Ta có: 
Suy ra: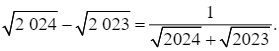 
⦁ Ta có: 
Suy ra: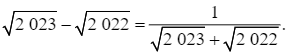 
Do 2024 > 2022 nên 
Do đó 
Do đó: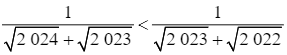 
Hay 
Lời giải
Gọi x (cm) là độ dài cạnh của hình vuông với x > 0.
Do hai cạnh của một hình vuông và đường chéo tạo thành một tam giác vuông nên áp dụng định lý Pythagore ta có:
x2 + x2 = 2x2.
Khi đó, độ dài đường chéo của hình vuông đó là 
Do độ dài đường chéo của một hình vuông lớn hơn độ dài cạnh của nó là 4 cm nên ta có phương trình: 
Giải phương trình:
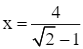
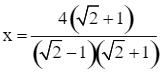
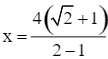
(thoả mãn x > 0).
Vậy độ dài cạnh của hình vuông đó là 
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo