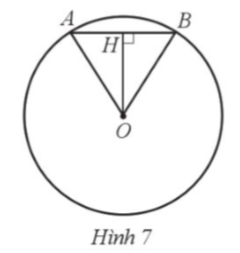
Hai hòn đảo được xem như hai hình tròn có khoảng cách từ tâm hòn đảo này đến tâm hòn đảo kia là khoảng 950 m. Biết rằng hòn đảo lớn có bán kính khoảng 500 m, còn đảo nhỏ có bán kính khoảng 300 m. Người ta cần xây dựng một cây cầu bắc từ đảo này sang đảo kia. Hãy chọn vị trí để xây cầu sao cho chiều dài cây cầu là ngắn nhất, khi đó tính chiều dài cây cầu.
Hai hòn đảo được xem như hai hình tròn có khoảng cách từ tâm hòn đảo này đến tâm hòn đảo kia là khoảng 950 m. Biết rằng hòn đảo lớn có bán kính khoảng 500 m, còn đảo nhỏ có bán kính khoảng 300 m. Người ta cần xây dựng một cây cầu bắc từ đảo này sang đảo kia. Hãy chọn vị trí để xây cầu sao cho chiều dài cây cầu là ngắn nhất, khi đó tính chiều dài cây cầu.
Quảng cáo
Trả lời:
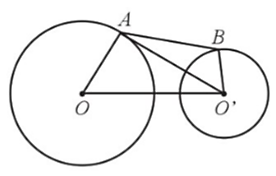
Gọi hòn đảo lớn là đường tròn (O; 500 m) và hòn đảo nhỏ là đường tròn (O’; 300 m). Lấy A thuộc đường tròn (O) và B thuộc đường tròn tâm (O’) là hai vị trí đầu cầu (hình vẽ).
Khi đó, AB là chiều dài cây cầu và OO’ = 950 m, OA = 500 m, O’B = 300 m.
Xét ba điểm O’, A, B, ta có: AB ≥ O’A ‒ O’B.
Xét ba điểm O, O’, A, ta có: O’A ≥ OO’ ‒ OA.
Do đó AB ≥ OO’ ‒ OA ‒ O’B hay AB ≥ 150 m.
Dấu “=“ xảy ra khi bốn điểm O, A, B, O’ thẳng hàng theo thứ tự đó.
Vậy ta nên đặt cầu trên đoạn nối tâm của hai đảo thì cây cầu có chiều dài ngắn nhất là 150 m.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
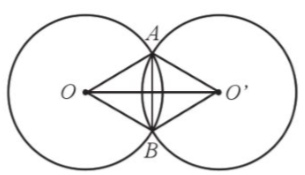
Tứ giác OAO’B có OA = OB = O’A = O’B (cùng bằng bán kính của (O) và (O’))
Suy ra tứ giác OAO’B là hình thoi.
Do đó hai đường chéo AB và OO’ cắt nhau tại trung điểm của mỗi đường.
Lời giải
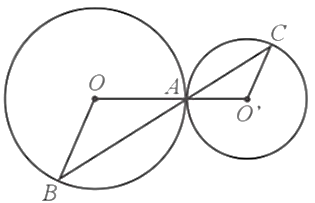
a) Vì A, B ∈ (O; 3 cm) nên OA = OB = 3 cm.
Do đó ∆OAB cân tại O, suy ra (1)
Vì A, C ∈ (O’; 2 cm) nên O’A = O’C = 2 cm.
Do đó ∆O’AC cân tại O’, suy ra (2)
Mà (đối đỉnh) (3)
Từ (1), (2), (3) suy ra hay
Mà hai góc này ở vị trí so le trong nên OB // O’C.
b) Vì OB // O’C nên theo định lí Thalès ta có hay
Do đó
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.