Câu hỏi:

25/07/2024 8,364

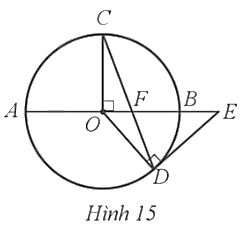
Cho đường tròn tâm O đường kính AB = 2R, bán kính OC vuông góc với AB tại O. Lấy điểm F thuộc đoạn thẳng OB, tia CF cắt đường tròn (O) tại D. Tiếp tuyến tại D của đường tròn (O) cắt AB tại E (Hình 15). Chứng minh EF = ED.

Xem lời giải

Câu hỏi trong đề: Giải SBT Toán 9 Cánh Diều Bài 2. Vị trí tương đối của đường thẳng và đường tròn !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Do OC = OD nên ∆OCD cân tại O, suy ra $\hat{O C D} = \hat{O D C}$ hay $\hat{O C F} = \hat{O D F} .$

Xét ∆COF vuông tại O có $\hat{O C F} + \hat{O F C} = 90 °$ (tổng hai góc nhọn trong)

Lại có $\hat{O F C} = \hat{D F E}$ (đối đỉnh)

Suy ra $\hat{O D F} + \hat{D F E} = 90 °$

Mà $\hat{O D F} + \hat{F D E} = 90 °$ nên $\hat{D F E} = \hat{F D E} .$

Do đó ∆EDF cân tại E, suy ra EF = ED.

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho đường tròn (O; R) và điểm A sao cho OA = 2R. Kẻ tiếp tuyến AB của đường tròn (O; R) với B là tiếp điểm (Hình 14). Tính độ dài đoạn thẳng AB theo R.

Xem đáp án

Lời giải

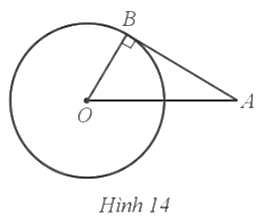
Do AB của đường tròn (O; R) với B là tiếp điểm nên OB ⊥ AB tại B.

Xét ∆OAB vuông tại B, theo định lí Pythagore, ta có:

OA² = OB² + AB²

Suy ra $A B = \sqrt{O A^{2} - O B^{2}} = \sqrt{{(2 R)}^{2} - R^{2}} = \sqrt{3 R^{2}} = R \sqrt{3} .$

Vậy $A B = R \sqrt{3} .$

Câu 2

Từ điểm A ở ngoài đường tròn (O) vẽ tiếp tuyến AB của đường tròn với B là tiếp điểm. Lấy các điểm C, D thuộc đường tròn (O) sao cho C nằm giữa A và D, O không thuộc AD. Gọi I là trung điểm của đoạn thẳng CD, tia OI cắt AB tại E (Hình 16). Chứng minh:

a) EB . EA = EI . EO;

b) AB² = AC . AD.

Xem đáp án

Lời giải

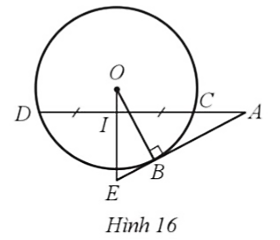
a) Xét ∆OCD có OC = OD nên ∆OCD cân tại O, suy ra đường trung tuyến OI của tam giác cũng đồng thời là đường cao, hay $\hat{O I C} = \hat{O I D} = 90 ° .$

Do AB là tiếp tuyến của đường tròn (O) với B là tiếp điểm nên OB ⊥ AB. Suy ra $\hat{O B E} = 90 °$

Xét ∆EOB và ∆EAI có:

$\hat{O B E} = \hat{E I A} (= 90 °)$ và $\hat{E}$ là góc chung

Do đó ∆EOB ᔕ ∆EAI (g.g)

Suy ra $\frac{E B}{E I} = \frac{E O}{E A}$ hay EB . EA = EI . EO.

b) Gọi R là bán kính đường tròn (O).

Xét ∆OAB vuông tại B, theo định lí Pythagore, ta có: OA² = OB² + AB²

Suy ra AB² = OA² ‒ OB² = OA² ‒ R².

Mặt khác, ta có: AC.AD = (AI ‒ CI)(AI + DI)

Mà CI = DI (do I là trung điểm của CD)

Suy ra: AC.AD = (AI ‒ CI)(AI + CI) = AI² ‒ CI²

Xét ∆OAI vuông tại I, theo định lí Pythagore, ta có: OA² = OI² + AI²

Suy ra AI² = OA² ‒ OI².

Xét ∆OCI vuông tại I, theo định lí Pythagore, ta có: OC² = OI² + CI²

Suy ra CI² = OC² ‒ OI².

Do đó AC.AD = (OA² ‒ OI²) ‒ (OC² ‒ OI²)

= OA² ‒ OI² ‒ OC² + OI²

= OA² – OC² = OA² ‒ R².

Do đó AB² = AC. AD (vì cùng bằng OA² ‒ R²).

Câu 3

Cho đường thẳng a và điểm O với khoảng cách từ điểm O đến đường thẳng a là 1 cm. Vẽ đường tròn tâm O bán kính 3 cm.

a) Xác định vị trí tương đối của đường thẳng a và đường tròn (O).

b) Gọi A và B là các giao điểm của đường thẳng a và đường tròn (O). Tính độ dài đoạn thẳng AB.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hình vuông ABCD. Trên đường chéo BD, lấy điểm H sao cho BH = AB. Qua điểm H kẻ đường thẳng vuông góc với BD cắt AD tại O.

a) So sánh OA, OH, HD.

b) Xác định vị trí tương đối của BD và đường tròn (O; OA).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho đường tròn (O; 4 cm) và đường thẳng d sao cho khoảng cách từ điểm O đến đường thẳng d là OH = 5 cm. Đường thẳng OH cắt đường tròn (O) tại A. Gọi B là trung điểm của đoạn thẳng OA. Trên đường thẳng d, lấy một điểm I (khác H), kẻ tiếp tuyến IC của đường tròn (O) với C là tiếp điểm (Hình 17). Chứng minh tam giác IBC cân tại I.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hình thang vuông ABCD $(\hat{A} = \hat{D} = 90 °)$ có AB = 4 cm, BC = 13 cm, CD = 9 cm.

a) Tính độ dài đoạn thẳng AD.

b) Đường thẳng AD có tiếp xúc với đường tròn đường kính BC hay không? Vì sao?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Cho đường tròn tâm O đường kính AB = 2R, bán kính OC vuông góc với AB tại O. Lấy điểm F thuộc đoạn thẳng OB, tia CF cắt đường tròn (O) tại D. Tiếp tuyến tại D của đường tròn (O) cắt AB tại E (Hình 15). Chứng minh EF = ED.

Bình luận

Cho đường tròn (O; R) và điểm A sao cho OA = 2R. Kẻ tiếp tuyến AB của đường tròn (O; R) với B là tiếp điểm (Hình 14). Tính độ dài đoạn thẳng AB theo R.

Cho hình vuông ABCD. Trên đường chéo BD, lấy điểm H sao cho BH = AB. Qua điểm H kẻ đường thẳng vuông góc với BD cắt AD tại O. a) So sánh OA, OH, HD. b) Xác định vị trí tương đối của BD và đường tròn (O; OA).

Cho hình thang vuông ABCD A^=D^=90° có AB = 4 cm, BC = 13 cm, CD = 9 cm. a) Tính độ dài đoạn thẳng AD. b) Đường thẳng AD có tiếp xúc với đường tròn đường kính BC hay không? Vì sao?

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho hình vuông ABCD. Trên đường chéo BD, lấy điểm H sao cho BH = AB. Qua điểm H kẻ đường thẳng vuông góc với BD cắt AD tại O.

a) So sánh OA, OH, HD.

b) Xác định vị trí tương đối của BD và đường tròn (O; OA).

Cho hình thang vuông ABCD $(\hat{A} = \hat{D} = 90 °)$ có AB = 4 cm, BC = 13 cm, CD = 9 cm.

a) Tính độ dài đoạn thẳng AD.

b) Đường thẳng AD có tiếp xúc với đường tròn đường kính BC hay không? Vì sao?