Cho đường tròn (O; R) và hai điểm A, B nằm trên đường tròn sao cho độ dài cung nhỏ AB bằng 5πR6. a) Xác định điểm C trên cung lớn AB sao cho khi kẻ CH vuông góc với AB tại H thì AH = CH. b) Tính độ d...

a) Đặt AOB^=n°. Khi đó, ta có sđAB⏜=n°. Ta có công thức tính độ dài cung tròn n° trong đường tròn bán kính R là: l=πRn180. Do độ dài cung nhỏ AB bằng 5πR6 nên ta có πRn180=5πR6, suy ra n=180⋅56=150. Suy ra AOB^=150° hay sđAB⏜=150°. Tam giác ACH có AHC^=90° và AH = CH nên tam giác ACH vuông cân tại H. Suy ra BAC^=45°. Do đó sđBC⏜=2BAC^=2⋅54°=90°. Vậy điểm C trên cung lớn AB sao cho sđBC⏜=90° thì AH = CH. b) Ta có: ⦁ sđACB⏜=360°−sđAB⏜=360°−150°=210°. ⦁sđACB⏜=sđAC⏜+sđCB⏜ Suy ra sđAC⏜=sđACB⏜−sđCB⏜=210°−90°=120°. Độ dài cung nhỏ AC là: l1=πR⋅120180=2πR3 (đơn vị độ dài). Độ dài cung nhỏ BC là: l2=πR⋅90180=πR2 (đơn vị độ dài). c) Xét ∆OAB cân tại O (do OA = OB) nên đường cao OK đồng thời là đường phân giác của tam giác, do đó sđEB⏜=EOB^=12AOB^=12⋅150°=75°. Diện tích hình quạt tròn EOB là S=πR2⋅75360=5πR224 (đơn vị diện tích). d) Diện tích hình quạt tròn BOC là S1=πR2⋅90360=πR24 (đơn vị diện tích). Diện tích hình quạt AOC là S2=πR2⋅120360=πR23 (đơn vị diện tích). Vậy tỉ số phần trăm giữa diện tích hình quạt tròn BOC và diện tích hình quạt tròn AOC là: S1S2⋅100%=πR24:πR23⋅100%=75%.

Câu hỏi:

02/08/2024 2,860

Cho đường tròn (O; R) và hai điểm A, B nằm trên đường tròn sao cho độ dài cung nhỏ AB bằng $\frac{5 π R}{6} .$

a) Xác định điểm C trên cung lớn AB sao cho khi kẻ CH vuông góc với AB tại H thì AH = CH.

b) Tính độ dài các cung AC, BC theo R.

c) Kẻ OK vuông góc với AB tại K, tia OK cắt đường tròn (O) tại E. Tính diện tích hình quạt tròn EOB (giới hạn bởi cung nhỏ BE và hai bán kính OE, OB ) theo R.

d) Tính tỉ số phần trăm giữa diện tích hình quạt tròn BOC (giới hạn bởi cung nhỏ BC và hai bán kính OB, OC) và diện tích hình quạt tròn AOC (giới hạn bởi cung nhỏ AC và hai bán kính OA, OC).

Xem lời giải

Câu hỏi trong đề: Giải SBT Toán 9 Cánh Diều BÀI TẬP CUỐI CHƯƠNG V !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

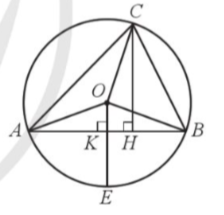
Media VietJack

a) Đặt $\hat{A O B} = n ° .$ Khi đó, ta có $s đ \overset{⏜}{A B} = n ° .$

Ta có công thức tính độ dài cung tròn n° trong đường tròn bán kính R là: $l = \frac{π R n}{180} .$

Do độ dài cung nhỏ AB bằng $\frac{5 π R}{6}$ nên ta có $\frac{π R n}{180} = \frac{5 π R}{6},$ suy ra $n = \frac{180 \cdot 5}{6} = 150.$

Suy ra $\hat{A O B} = 150 °$ hay $s đ \overset{⏜}{A B} = 150 ° .$

Tam giác ACH có $\hat{A H C} = 90 °$ và AH = CH nên tam giác ACH vuông cân tại H.

Suy ra $\hat{B A C} = 45 ° .$

Do đó $s đ \overset{⏜}{B C} = 2 \hat{B A C} = 2 \cdot 54 ° = 90 ° .$

Vậy điểm C trên cung lớn AB sao cho $s đ \overset{⏜}{B C} = 90 °$ thì AH = CH.

b) Ta có:

⦁ $sđ \overset{⏜}{A C B} = 360 ° - sđ \overset{⏜}{A B} = 360 ° - 150 ° = 210 ° .$

⦁ $s đ \overset{⏜}{A C B} = s đ \overset{⏜}{A C} + s đ \overset{⏜}{C B}$

Suy ra $s đ \overset{⏜}{A C} = s đ \overset{⏜}{A C B} - s đ \overset{⏜}{C B} = 210 ° - 90 ° = 120 ° .$

Độ dài cung nhỏ AC là: $l_{1} = \frac{π R \cdot 120}{180} = \frac{2 π R}{3}$ (đơn vị độ dài).

Độ dài cung nhỏ BC là: $l_{2} = \frac{π R \cdot 90}{180} = \frac{π R}{2}$ (đơn vị độ dài).

c) Xét ∆OAB cân tại O (do OA = OB) nên đường cao OK đồng thời là đường phân giác của tam giác, do đó $sđ \overset{⏜}{E B} = \hat{E O B} = \frac{1}{2} \hat{A O B} = \frac{1}{2} \cdot 150 ° = 75 ° .$

Diện tích hình quạt tròn EOB là $S = \frac{π R^{2} \cdot 75}{360} = \frac{5 π R^{2}}{24}$ (đơn vị diện tích).

d) Diện tích hình quạt tròn BOC là $S_{1} = \frac{π R^{2} \cdot 90}{360} = \frac{π R^{2}}{4}$ (đơn vị diện tích).

Diện tích hình quạt AOC là $S_{2} = \frac{π R^{2} \cdot 120}{360} = \frac{π R^{2}}{3}$ (đơn vị diện tích).

Vậy tỉ số phần trăm giữa diện tích hình quạt tròn BOC và diện tích hình quạt tròn AOC là: $\frac{S_{1}}{S_{2}} \cdot 100 % = (\frac{π R^{2}}{4} : \frac{π R^{2}}{3}) \cdot 100 % = 75 % .$

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hai đường tròn (O; R) và (O’; R) cắt nhau tại hai điểm M, N với OO’ = 24 cm và MN = 10 cm (Hình 52). Khi đó, R bằng:

A. 26 cm.

B. 13 cm.

C. 14 cm.

D. 34 cm.

Xem đáp án

Lời giải

Đáp án đúng là: B

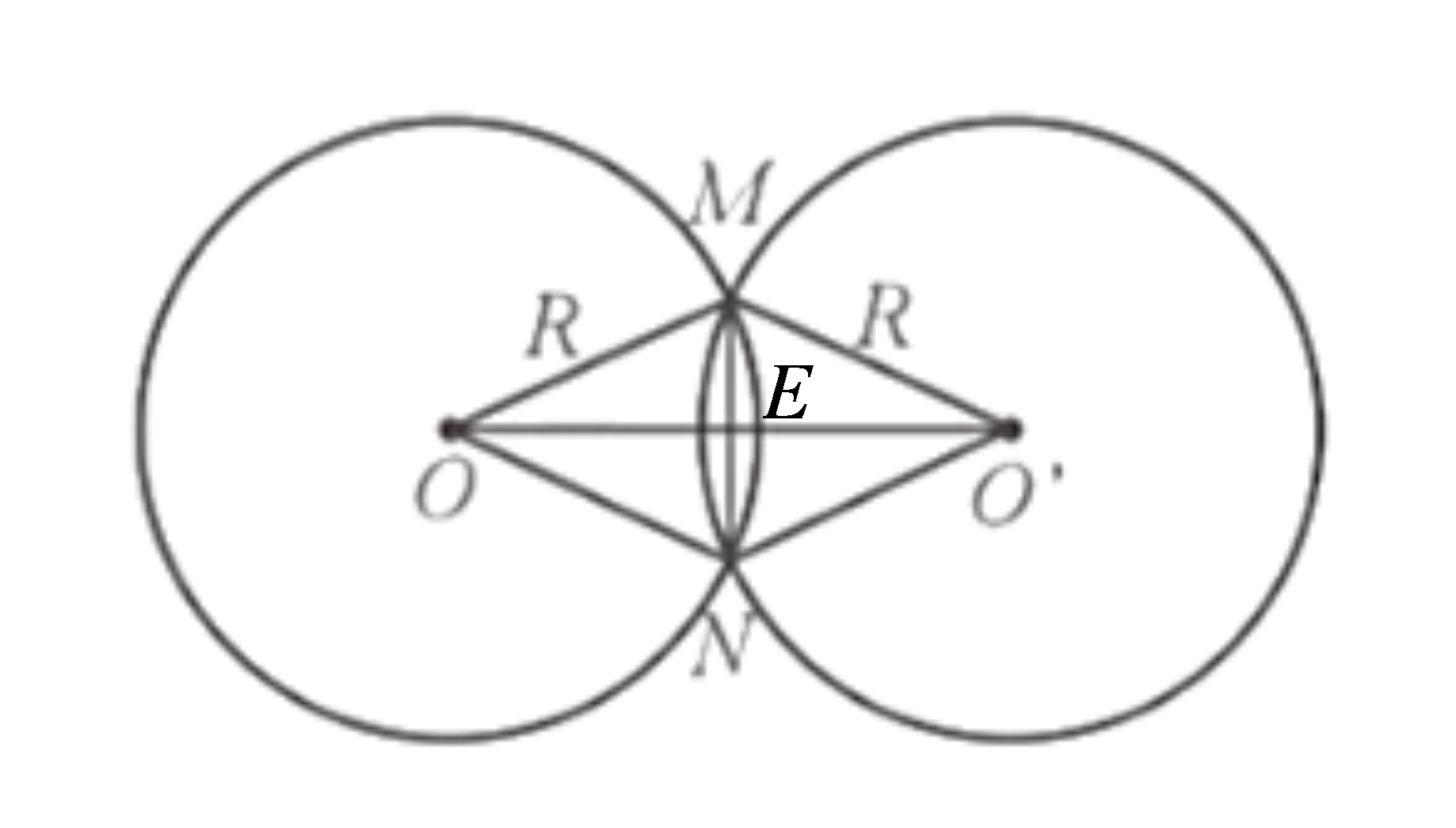
Media VietJack

Gọi E là giao điểm của MN và OO’.

Ta có: OM = ON = R (bán kính đường tròn (O; R)) và O’M = O’N = R (bán kính đường tròn (O’; R)). Suy ra OM = ON = O’M = O’N, nên OMO’N là hình thoi.

Do đó hai đường chéo MN và OO’ vuông góc với nhau tại trung điểm E của mỗi đường.

Suy ra $O E = \frac{1}{2} = \frac{1}{2} \cdot 24 = 12 (c m)$ và $M E = \frac{1}{2} MN = \frac{1}{2} \cdot 10 = 5 (c m) .$

Xét ∆OME vuông tại E, theo định lí Pythagore, ta có:

OM² = OE² + ME²

Suy ra $O M = \sqrt{O E^{2} + M E^{2}} = \sqrt{12^{2} + 5^{2}} = \sqrt{169} = 13 (c m) .$

Vậy R = 13 cm.

Câu 2

Cho đường tròn tâm O đường kính AB và điểm M di chuyển trên đường tròn (M khác A và B). Vẽ đường tròn (M) tiếp xúc với AB tại H. Từ A và B kẻ hai tiếp tuyến AC, BD của đường tròn (M) lần lượt tại C, D.

a) Chứng minh AC + BD không đổi khi M di chuyển trên đường tròn (O).

b) Chứng minh CD là tiếp tuyến của đường tròn (O).

Xem đáp án

Lời giải

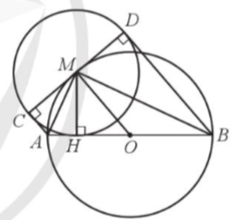
Media VietJack

a) Do AC, AH là hai tiếp tuyến của đường tròn (M) nên AC = AH.

Tương tự, ta chứng minh được BD = BH.

Do đó AC + BD = AH + BH = AB (không đổi).

b) ⦁ Do AC, AH là hai tiếp tuyến của đường tròn (M) nên MA là tia phân giác của góc CMH hay $\hat{A M C} = \hat{A M H} .$

Tương tự, ta chứng minh được $\hat{B M D} = \hat{B M H} .$

Xét đường tròn (O) đường kính AB có $\hat{A M B} = 90 °$ (góc nội tiếp chắn nửa đường tròn).

Mà $\hat{A M H} + \hat{B M H} = \hat{A M B} = 90 °$

Suy ra $\hat{C M D} = \hat{A M C} + \hat{A M H} + \hat{B M H} + \hat{B M D} = 2 (\hat{A M H} + \hat{B M H}) = 2 \cdot 90 ° = 180 °$

Do đó ba điểm C, M, D thẳng hàng.

⦁ Do tam giác OBM cân tại O (do OM = OB) nên $\hat{O B M} = \hat{O M B} .$

Suy ra $2 \hat{O B M} + \hat{B O M} = 180 ° .$

Ta lại có: $\hat{A O M} + \hat{B O M} = 180 °$ nên $\hat{A O M} = 2 \hat{O B M} .$

Lại có BM là tia phân giác của góc ABD (do hai tiếp tuyến BD, BH của (O) cắt nhau tại B) hay $\hat{A B D} = 2 \hat{O B M} .$

Suy ra $\hat{A O M} = \hat{A B D} .$

Mà hai góc này ở vị trí đồng vị nên OM // BD.

Mặt khác, BD ⊥ CD (do BD ⊥ CM) nên CD vuông góc với OM tại M thuộc đường tròn (O).

Vậy CD là tiếp tuyến của đường tròn (O).

Câu 3

Cho ba đường tròn (A; 10 cm), (B; 15 cm), (C; 15 cm) tiếp xúc ngoài với nhau đôi một. Đường tròn (A) tiếp xúc với (B) và (C) lần lượt tại C’ và B’. Đường tròn (B) tiếp xúc với (C) tại A’ (Hình 53).

a) Chứng minh AA’ là tiếp tuyến chung của đường tròn (B) và (C).

b) Tính độ dài đoạn thẳng AA’ và diện tích tam giác AB’C’.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho nửa đường tròn tâm O đường kính A B. Gọi C, D lần lượt là điểm chính giữa của cung AB, AC.

a) Chứng minh $\hat{B A C} = \hat{C O D} = \hat{A B C} = \hat{A C O} .$

b) Lấy điểm M thuộc cung CD. Chứng minh AM > CM và $\hat{C O M} = 2 \hat{C A M} .$

c) Khi M di chuyền trên cung nhỏ AC, tìm vị trí của điểm M để diện tích của tam giác MAC lớn nhất.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho đường tròn (O; R) và ba điểm A, B, C nằm trên đường tròn với AB < AC. Gọi M là trung điểm của đoạn thẳng BC. Trên cung BC không chứa điểm A, lấy điểm D sao cho $\hat{B A D} = \hat{C A M} .$

a) Chứng minh $\hat{A D B} = \hat{C D M} .$

b) Gọi E là giao điểm của tia OM và cung BC. Tính diện tích hình quạt tròn giới hạn bởi các bán kính OE, OC và cung nhỏ CE theo R, biết $B C = R \sqrt{2} .$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Trong 20 giây, bánh xe của một chiếc xe máy quay được 80 vòng. Độ dài bán kính của bánh xe đó là 25 cm. Khi đó, quãng đường xe máy đi được trong 3 phút là:

A. 36 000π m.

B. 360π m.

C. 18 000π m.

D. 180π m.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Cho hai đường tròn (O; R) và (O’; R) cắt nhau tại hai điểm M, N với OO’ = 24 cm và MN = 10 cm (Hình 52). Khi đó, R bằng:

A. 26 cm.

B. 13 cm.

C. 14 cm.

D. 34 cm.

Trong 20 giây, bánh xe của một chiếc xe máy quay được 80 vòng. Độ dài bán kính của bánh xe đó là 25 cm. Khi đó, quãng đường xe máy đi được trong 3 phút là:

A. 36 000π m.

B. 360π m.

C. 18 000π m.

D. 180π m.