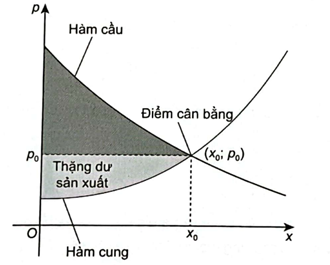
Ta đã biết rằng hàm cầu liên quan đến giá p của một sản phẩm mới với nhu cầu của người tiêu dùng, hàm cung liên quan đến giá p của sản phẩm với mức độ sẵn sàng cung cấp sản phẩm của nhà sản xuất. Điểm cắt nhau (x₀; p₀) của đồ thị hàm cầu y = D(x) và đồ thị hàm cung p = S(x) được gọi là điểm cân bằng. các nhà kinh tế gọi diện tích của hình giới hạn bởi đồ thị hàm cầu, đường ngang p = p₀ và đường thẳng đứng x = 0 là thặng dư tiêu dùng. Tương tự, diện tích của hình giới hạn bởi đồ thị của hàm cung, đường nằm ngang p = p₀ và đường thẳng đứng x = 0 được gọi là thặng dư sản xuất, như trong hình vẽ sau:

Giả sử hàm cung và hàm cầu của một loại sản phẩm được mô hình hóa bởi:

Hàm cầu: y = −0,01e² + 19 và hàm cung: p = 0,09e^x + 1 trong đó x là số đơn vị sản phẩm. Thặng dư tiêu dung và thặng dư dản xuất cho sản phẩm này lần lượt là (Làm tròn kết quả đến chữ số thập phân thứ hai).

A. 68,01 và 7,57.

B. 68,02 và 7,56.

C. 69,02 và 7,56.

D. 79,02 và 7,66.

Xem lời giải

Câu hỏi trong đề: Giải SBT Toán 12 Tập 2 KNTT Đề minh họa Kiểm tra cuối học kì II có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án đúng là: B

Hoành độ điểm cân bằng là nghiệm của phương trình

−0,01e^x + 19 = 0,09e^x + 1

⇒ 0,1e^x = 18 ⇒ x = ln180.

Suy ra tung độ điểm cân bằng y = 0,09e^ln180 + 1 = 17,2.

Thặng dư sản xuất cho sản phẩm đã cho là:

\(\int\limits_0^{\ln 180} {\left| {17,2 - 0,09{e^x} - 1} \right|dx} \) ≈ 68,02.

Thặng dư tiêu dùng cho sản phẩm đã cho là:

\(\int\limits_0^{\ln 180} {\left| { - 0,01{e^x} + 19 - 17,2} \right|dx} \) ≈ 7,56.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Có hai đội thi đấu môn bắn súng. Đội I có 6 vận động viên, dội II có 8 vận động viên. Xác suất đạt huy chương vàng của mỗi vận động viên của đội I và đội II tương ứng là 0,65 và 0,55. Chọn ngẫu nhiên một vận động viên trong hai đội. Giả sử vận động viên được chọn đạt huy chương vàng. Tính xác suất để vận động viên này thuộc đội I.

A. \(\frac{{49}}{{140}}\).

B. \(\frac{{39}}{{83}}\).

C. \(\frac{{43}}{{83}}\).

D. \(\frac{{37}}{{140}}\).

Xem đáp án

Lời giải

Đáp án đúng là: B

Gọi A là biến cố: “Vận động viên được chọn đội I”.

B là biến cố: “Vận động viên đạt huy chương vàng”.

Ta có: P(A) = \(\frac{6}{{14}} = \frac{3}{7}\); P(\(\overline A \)) = 1 – P(A) = \(\frac{4}{7}\);

P(B | A) = 0,65; P(B | \(\overline A \)) = 0,55.

Xác suất để vận động viên được chọn thuộc đội I khi vận động viên ấy đạt huy chương vàng được tính theo công thức Bayes là:

P(A | B) = \(\frac{{P\left( A \right).P\left( {A|B} \right)}}{{P\left( A \right).P\left( {A|B} \right) + P\left( {\overline A } \right).P\left( {A|\overline A } \right)}}\) = \(\frac{{\frac{3}{7}.0,65}}{{\frac{3}{7}.0,65 + \frac{4}{7}0,55}} = \frac{{39}}{{83}}\).

Câu 2

Góc quan sát ngang của một camera là 130°. Trong không gian Oxyz, camera được đặt tại điểm C(1; 2; 2) và chiếu thẳng về phía mặt phẳng (P): x + 2y – 2z + 5 = 0. Hỏi vùng quan sát được trên mặt phẳng (P) của camera là hình tròn có diện tích bằng bao nhiêu? (Làm tròn kết quả đến chữ số hàng thập phân thứ nhất).

A. 57,7.

B. 57,8.

C. 56,7.

D. 56,8.

Xem đáp án

Lời giải

Đáp án đúng là: B

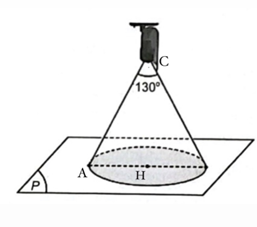
Góc quan sát ngang của một camera là 130°. Trong không gian Oxyz, camera được đặt tại điểm C(1; 2; 2) và chiếu thẳng về phía mặt phẳng (P): x + 2y – 2z + 5 = 0. (ảnh 2)

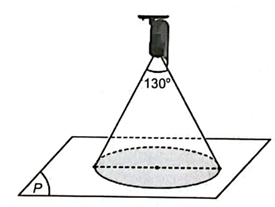
Gọi H là hình chiếu của C trên mặt phẳng (P).

Khoảng cách từ điểm C tới mặt phẳng (P) là d(C; (P)) = CH = \(\frac{{\left| {1.1 + 2.2 - 2.2 + 5} \right|}}{{\sqrt {{1^2} + {2^2} + {2^2}} }}\) = 2.

Vùng quan sát là hình tròn tâm H bán kính HA.

Ta có tam giác AHC cân tại C có CH vuông với đáy nên \(\widehat {ACH}\) = \(\frac{1}{2}\widehat C\) = 65°.

Do đó, AH = CH.tan65°.

Vậy diện tích vùng quan sát là: π.(CH.tan65°)² ≈ 57,8.

Câu 3