Một ô tô đang chạy với vận tốc 10 m/s thì người lái đạp phanh; từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc v(t) = −5t + 10 (m/s), trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét?
A. 0,2 m.
B. 2 m.
C. 10 m.
D. 20 m.
Một ô tô đang chạy với vận tốc 10 m/s thì người lái đạp phanh; từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc v(t) = −5t + 10 (m/s), trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét?
A. 0,2 m.
B. 2 m.
C. 10 m.
D. 20 m.
Quảng cáo
Trả lời:
Đáp án đúng là: C
Xét v(t) = 0 ⇔ −5t + 10 = 0 ⇔ t = 2.
Do vậy, kể từ lúc người lại đạp phanh thì sau 2 giây ô tô dùng hẳn.
Quãng đường ô tô đi được kể từ lúc người lái đạp phanh đến khi ô tô dừng hẳn là:
s = \(\int\limits_0^2 {\left( { - 5t + 10} \right)dt = \left. {\left( { - \frac{5}{2}{t^2} + 10t} \right)} \right|_0^2} \)= 10 (m).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: B
Gọi A là biến cố: “Vận động viên được chọn đội I”.
B là biến cố: “Vận động viên đạt huy chương vàng”.
Ta có: P(A) = \(\frac{6}{{14}} = \frac{3}{7}\); P(\(\overline A \)) = 1 – P(A) = \(\frac{4}{7}\);
P(B | A) = 0,65; P(B | \(\overline A \)) = 0,55.
Xác suất để vận động viên được chọn thuộc đội I khi vận động viên ấy đạt huy chương vàng được tính theo công thức Bayes là:
P(A | B) = \(\frac{{P\left( A \right).P\left( {A|B} \right)}}{{P\left( A \right).P\left( {A|B} \right) + P\left( {\overline A } \right).P\left( {A|\overline A } \right)}}\) = \(\frac{{\frac{3}{7}.0,65}}{{\frac{3}{7}.0,65 + \frac{4}{7}0,55}} = \frac{{39}}{{83}}\).
Lời giải
Đáp án đúng là: B
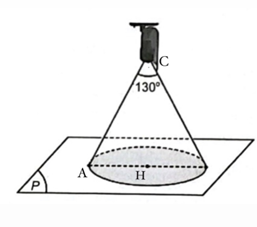
Gọi H là hình chiếu của C trên mặt phẳng (P).
Khoảng cách từ điểm C tới mặt phẳng (P) là d(C; (P)) = CH = \(\frac{{\left| {1.1 + 2.2 - 2.2 + 5} \right|}}{{\sqrt {{1^2} + {2^2} + {2^2}} }}\) = 2.
Vùng quan sát là hình tròn tâm H bán kính HA.
Ta có tam giác AHC cân tại C có CH vuông với đáy nên \(\widehat {ACH}\) = \(\frac{1}{2}\widehat C\) = 65°.
Do đó, AH = CH.tan65°.
Vậy diện tích vùng quan sát là: π.(CH.tan65°)2 ≈ 57,8.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.