Biết rằng nếu vị trí M có vĩ độ và kinh độ tương ứng là α°N, β°E (0 < α, β < 90) thì có tọa độ M(cosα°cosβ°; cosα°sinβ°; sinα°). Biết 1 đơn vị dài trong không gian Oxyz tương ứng với 6 371 km trong thực tế. Khoảng cách trên mặt đất từ vị trí P: 30°N45°E đến vị trí Q: 60°N45°E là (tính chính xác tới chữ số thập phân thứ tư sau dấu phẩy theo đơn vị kilômét)

A. 3335,8475 km.

B. 3335,8478 km.

C. 3355,8478 km.

D. 3355,8475 km.

Xem lời giải

Câu hỏi trong đề: Giải SBT Toán 12 Tập 2 KNTT Đề minh họa Kiểm tra cuối học kì II có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án đúng là: B

Ta có: P: 30°N45°E thì P(cos30°cos45°; cos30°sin45°; sin30°) ⇒ P\(\left( {\frac{{\sqrt 6 }}{4};\frac{{\sqrt 6 }}{4};\frac{1}{2}} \right)\).

Q: 60°N45°E thì Q(cos60°cos45°; cos60°sin45°; sin60°) ⇒ Q\(\left( {\frac{{\sqrt 2 }}{4};\frac{{\sqrt 2 }}{4};\frac{{\sqrt 3 }}{2}} \right)\).

Từ đó, cos\(\left( {\widehat {POQ}} \right)\) = \(\frac{{\overrightarrow {OP} .\overrightarrow {OQ} }}{{\left| {\overrightarrow {OP} } \right|.\left| {\overrightarrow {OQ} } \right|}} = \frac{{\sqrt 3 }}{2}\) ⇒ \(\widehat {POQ}\) = 30°.

Khoảng cách trên mặt đất từ P tới Q là:

\(\frac{{30.2\pi }}{{360}}.6371\) ≈ 3 335,8478 km.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Có hai đội thi đấu môn bắn súng. Đội I có 6 vận động viên, dội II có 8 vận động viên. Xác suất đạt huy chương vàng của mỗi vận động viên của đội I và đội II tương ứng là 0,65 và 0,55. Chọn ngẫu nhiên một vận động viên trong hai đội. Giả sử vận động viên được chọn đạt huy chương vàng. Tính xác suất để vận động viên này thuộc đội I.

A. \(\frac{{49}}{{140}}\).

B. \(\frac{{39}}{{83}}\).

C. \(\frac{{43}}{{83}}\).

D. \(\frac{{37}}{{140}}\).

Xem đáp án

Lời giải

Đáp án đúng là: B

Gọi A là biến cố: “Vận động viên được chọn đội I”.

B là biến cố: “Vận động viên đạt huy chương vàng”.

Ta có: P(A) = \(\frac{6}{{14}} = \frac{3}{7}\); P(\(\overline A \)) = 1 – P(A) = \(\frac{4}{7}\);

P(B | A) = 0,65; P(B | \(\overline A \)) = 0,55.

Xác suất để vận động viên được chọn thuộc đội I khi vận động viên ấy đạt huy chương vàng được tính theo công thức Bayes là:

P(A | B) = \(\frac{{P\left( A \right).P\left( {A|B} \right)}}{{P\left( A \right).P\left( {A|B} \right) + P\left( {\overline A } \right).P\left( {A|\overline A } \right)}}\) = \(\frac{{\frac{3}{7}.0,65}}{{\frac{3}{7}.0,65 + \frac{4}{7}0,55}} = \frac{{39}}{{83}}\).

Câu 2

Góc quan sát ngang của một camera là 130°. Trong không gian Oxyz, camera được đặt tại điểm C(1; 2; 2) và chiếu thẳng về phía mặt phẳng (P): x + 2y – 2z + 5 = 0. Hỏi vùng quan sát được trên mặt phẳng (P) của camera là hình tròn có diện tích bằng bao nhiêu? (Làm tròn kết quả đến chữ số hàng thập phân thứ nhất).

A. 57,7.

B. 57,8.

C. 56,7.

D. 56,8.

Xem đáp án

Lời giải

Đáp án đúng là: B

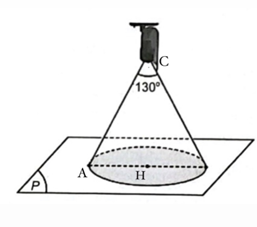
Góc quan sát ngang của một camera là 130°. Trong không gian Oxyz, camera được đặt tại điểm C(1; 2; 2) và chiếu thẳng về phía mặt phẳng (P): x + 2y – 2z + 5 = 0. (ảnh 2)

Gọi H là hình chiếu của C trên mặt phẳng (P).

Khoảng cách từ điểm C tới mặt phẳng (P) là d(C; (P)) = CH = \(\frac{{\left| {1.1 + 2.2 - 2.2 + 5} \right|}}{{\sqrt {{1^2} + {2^2} + {2^2}} }}\) = 2.

Vùng quan sát là hình tròn tâm H bán kính HA.

Ta có tam giác AHC cân tại C có CH vuông với đáy nên \(\widehat {ACH}\) = \(\frac{1}{2}\widehat C\) = 65°.

Do đó, AH = CH.tan65°.

Vậy diện tích vùng quan sát là: π.(CH.tan65°)² ≈ 57,8.

Câu 3