Câu hỏi:
25/08/2024 334
Cho tam giác ABC và D là một điểm nằm trong tam giác. Kẻ DE song song với AB (E thuộc cạnh AC). Kẻ DF song song với BC (F thuộc cạnh AC).
a) Trong nhóm các điểm B, D, F, C và nhóm các điểm A, B, C, D, nhóm các điểm nào là 4 đỉnh của một tứ giác lồi? Vì sao?
b) Các điểm A, B, C, D, E có phải là các đỉnh của một ngũ giác lồi không? Vì sao?
Cho tam giác ABC và D là một điểm nằm trong tam giác. Kẻ DE song song với AB (E thuộc cạnh AC). Kẻ DF song song với BC (F thuộc cạnh AC).
a) Trong nhóm các điểm B, D, F, C và nhóm các điểm A, B, C, D, nhóm các điểm nào là 4 đỉnh của một tứ giác lồi? Vì sao?
b) Các điểm A, B, C, D, E có phải là các đỉnh của một ngũ giác lồi không? Vì sao?
Quảng cáo
Trả lời:
Giải bởi Vietjack
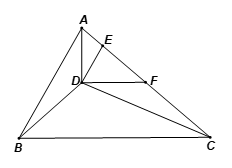
a) Bốn điểm B, D, F, C tạo thành tứ giác BDFC, đây là tứ giác lồi vì tứ giác BDFC nằm về một phía của đường thẳng chứa một cạnh bất kí của tứ giác đó.
Bốn điểm A, B, C, D tạo thành tứ giác ABCD, đây không phải là tứ giác lồi vì tứ giác ABCD nằm về hai phía của đường thẳng AD (hoặc đường thẳng CD).
b) Các điểm A, B, C, D, E tạo thành ngũ giác ABCDE, đây không phải là ngũ giác lồi vì ngũ giác ABCDE nằm về hai phía của đường thẳng CD (hoặc đường thẳng DE).
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
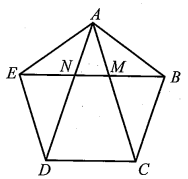
a) Ngũ giác ABCDE là ngũ giác đều nên AB = BC = CD = DE = EA và \(\widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEA} = \widehat {EAB}.\)
Ta cũng có tổng 5 góc của ngũ giác đều ABCDE bằng tổng các góc của ba tam giác ABC, ACD, ADE, tức là bằng 3.180° = 540°.
Do đó: \(\widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEA} = \widehat {EAB} = \frac{{540^\circ }}{5} = 108^\circ .\)
Xét ∆AEB cân tại A (do AB = AE) ta có:
\(\widehat {ABE} = \widehat {AEB} = \frac{{180^\circ - \widehat {EAB}}}{2} = \frac{{180^\circ - 108^\circ }}{2} = 36^\circ .\)
Hay \(\widehat {ABM} = \widehat {AEN} = 36^\circ .\)
Tương tự, đối với ∆EAD cân tại E ta có: \[\widehat {EAD} = \widehat {EDA} = 36^\circ \] hay \[\widehat {EAN} = 36^\circ .\]
Do đó ta có \[\widehat {EAN} = \widehat {NEA} = 36^\circ .\] Suy ra ∆AEN cân tại N.
Tương tự, ta chứng minh được ∆MAB cân tại M (do \(\widehat {MAB} = \widehat {MBA} = 36^\circ )\)
Suy ra \(\widehat {AMB} = 180^\circ - 2\widehat {MAB} = 180^\circ - 2 \cdot 36^\circ = 108^\circ .\)
Mặt khác: \(\widehat {CMB} = 180^\circ - \widehat {AMB} = 180^\circ - 108^\circ = 72^\circ ;\)
\(\widehat {MBC} = \widehat {ABC} - \widehat {ABM} = 108^\circ - 36^\circ = 72^\circ .\)
Suy ra tam giác CMB cân tại C.
b) Ta có: \(\widehat {EAB} = \widehat {EAN} + \widehat {NAM} + \widehat {MAB}\)
Suy ra \(\widehat {NAM} = \widehat {EAB} - \widehat {EAN} - \widehat {MAB} = 108^\circ - 36^\circ - 36^\circ = 36^\circ .\)
Do đó \(\widehat {EAN} = \widehat {NAM} = 36^\circ .\)
Vì vậy AN là phân giác của góc EAM.
c) Xét ∆MAB và ∆BAC có:
\(\widehat {AMB} = \widehat {ABC} = 108^\circ \) và \(\widehat {BAC}\) là góc chung
Do đó ∆MAB ᔕ ∆BAC (g.g), suy ra \(\frac{{AB}}{{AC}} = \frac{{BM}}{{CB}}\) hay AB.BC = BM.AC.
Lời giải
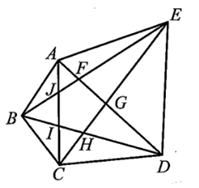
Áp dụng các bất đẳng thức tam giác ta có:
AF + FE > AE (trong tam giác AEF);
AJ + JB > AB (trong tam giác ABJ);
BI + IC > BC (trong tam giác BCI);
CH + HD > CD (trong tam giác CDH);
GE + GD > ED (trong tam giác GDE).
Do đó, ta có:
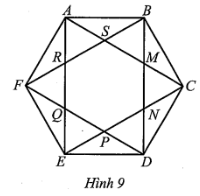
AF + FE + AJ + JB + BI + IC + CH + HD + GE + GD > AE + AB + BC + CD + ED. (1)
Mặt khác:
(AF + GD) + (JB + FE) + (AJ + IC) + (BI + HD) + (EG + CH) < AD + BE + AC + BD + EC.
Hay AF + FE + AJ + JB + BI + IC + CH + HD + GE + GD < AB + BC + CD + DE + EA. (2)
Từ (1) và (2) suy ra:
AC + AD + BD + BE + EC > AB + BC + CD + DE + EA.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
-
Chuyên đề 8: Hình học (có đáp án)