Câu hỏi:
25/08/2024 428
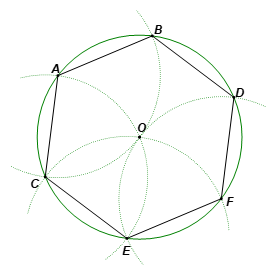
Người ta chia đường tròn (O; R) thành 6 cung bằng nhau như sau:
– Trên đường tròn (O; R), lấy điểm A tuỳ ý;
– Vẽ một phần đường tròn (A; R) cắt (O; R) tại B và C;
– Vẽ một phần đường tròn (C; R) cắt (O; R) tại E (khác A);
– Vẽ một phần đường tròn (E; R) cắt (O; R) tại F (khác C);
– Vẽ một phần đường tròn (F; R) cắt (O; R) tại D (khác E).
Nối A với B, B với D, D với F, F với E, E với C, C với A, ta được lục giác ABDFEC.
Chứng minh:
a) Lục giác ABDFEC là lục giác đều;
b) AF, BE, CD là các đường kính của đường tròn (O; R);
c) Các tứ giác ACEF, ABDC, BECA đều là hình thang cân.
Người ta chia đường tròn (O; R) thành 6 cung bằng nhau như sau:
– Trên đường tròn (O; R), lấy điểm A tuỳ ý;
– Vẽ một phần đường tròn (A; R) cắt (O; R) tại B và C;
– Vẽ một phần đường tròn (C; R) cắt (O; R) tại E (khác A);
– Vẽ một phần đường tròn (E; R) cắt (O; R) tại F (khác C);
– Vẽ một phần đường tròn (F; R) cắt (O; R) tại D (khác E).
Nối A với B, B với D, D với F, F với E, E với C, C với A, ta được lục giác ABDFEC.
Chứng minh:
a) Lục giác ABDFEC là lục giác đều;
b) AF, BE, CD là các đường kính của đường tròn (O; R);
c) Các tứ giác ACEF, ABDC, BECA đều là hình thang cân.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Nối OA, OB, OC, OD, OE, OF.
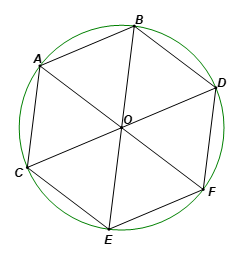
⦁ Từ giả thiết ta có sáu cung AB, AC, CE, EF, FD, DB bằng nhau nên \(\widehat {AOB} = \widehat {AOC} = \widehat {COE} = \widehat {EOF} = \widehat {FOD} = \widehat {DOB}.\)
Xét ∆AOB và ∆BOD có:
OA = OB; \(\widehat {AOB} = \widehat {BOD},\) OB = OD.
Do đó ∆AOB = ∆BOD (c.g.c), suy ra AB = BD (hai cạnh tương ứng).
Mặt khác, ta có AB = AC = CE = EF = FD = R.
Nên AB = AC = CE = EF = FD = DB. (1)
⦁ Ta có \(\widehat {AOB} + \widehat {AOC} + \widehat {COE} + \widehat {EOF} + \widehat {FOD} + \widehat {DOB} = 360^\circ \)
Suy ra \(6\widehat {AOB} = 360^\circ ,\) do đó \(\widehat {AOB} = 60^\circ .\)
Xét ∆AOB có OA = OB và \(\widehat {AOB} = 60^\circ \) nên ∆AOB là tam giác đều.
Do đó \(\widehat {OAB} = 60^\circ .\)
Chứng minh tương tự, ta cũng có ∆OAC đều nên \(\widehat {OAC} = 60^\circ .\)
Khi đó, \(\widehat {BAC} = \widehat {OAB} + \widehat {OAC} = 60^\circ + 60^\circ = 120^\circ .\)
Tương tự, ta chứng minh được:
\(\widehat {BAC} = \widehat {ACE} = \widehat {CEF} = \widehat {EFD} = \widehat {FDB} = \widehat {DBA} = 120^\circ .\,\,\,\left( 2 \right)\)
Từ (1) và (2) ta có ABDFEC là lục giác đều.
b) Do ABDFEC là lục giác đều nên ba đường chéo AF, BE, CD cắt nhau tại O.
Do đó AF, BE, CD là các đường kính của đường tròm (O; R).
c) Chứng minh tương tự ở câu a, ta chứng minh được ∆AOC, ∆OCE là các tam giác đều. Suy ra \(\widehat {AOC} = \widehat {OCE} = 60^\circ .\)
Mà hai góc này ở vị trí so le trong nên AO // CE hay AF // CE.
Tứ giác ACEF có AF // CE nên là hình thang.
Lại có \[\widehat {ACE} = \widehat {FEC} = 120^\circ \] nên ACEF là hình thang cân.
Chứng minh tương tự, ta cũng có các tứ giác ABDC, BECA đều là hình thang cân.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
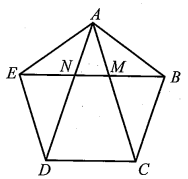
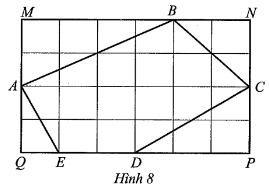
a) Ngũ giác ABCDE là ngũ giác đều nên AB = BC = CD = DE = EA và \(\widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEA} = \widehat {EAB}.\)
Ta cũng có tổng 5 góc của ngũ giác đều ABCDE bằng tổng các góc của ba tam giác ABC, ACD, ADE, tức là bằng 3.180° = 540°.
Do đó: \(\widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEA} = \widehat {EAB} = \frac{{540^\circ }}{5} = 108^\circ .\)
Xét ∆AEB cân tại A (do AB = AE) ta có:
\(\widehat {ABE} = \widehat {AEB} = \frac{{180^\circ - \widehat {EAB}}}{2} = \frac{{180^\circ - 108^\circ }}{2} = 36^\circ .\)
Hay \(\widehat {ABM} = \widehat {AEN} = 36^\circ .\)
Tương tự, đối với ∆EAD cân tại E ta có: \[\widehat {EAD} = \widehat {EDA} = 36^\circ \] hay \[\widehat {EAN} = 36^\circ .\]
Do đó ta có \[\widehat {EAN} = \widehat {NEA} = 36^\circ .\] Suy ra ∆AEN cân tại N.
Tương tự, ta chứng minh được ∆MAB cân tại M (do \(\widehat {MAB} = \widehat {MBA} = 36^\circ )\)
Suy ra \(\widehat {AMB} = 180^\circ - 2\widehat {MAB} = 180^\circ - 2 \cdot 36^\circ = 108^\circ .\)
Mặt khác: \(\widehat {CMB} = 180^\circ - \widehat {AMB} = 180^\circ - 108^\circ = 72^\circ ;\)
\(\widehat {MBC} = \widehat {ABC} - \widehat {ABM} = 108^\circ - 36^\circ = 72^\circ .\)
Suy ra tam giác CMB cân tại C.
b) Ta có: \(\widehat {EAB} = \widehat {EAN} + \widehat {NAM} + \widehat {MAB}\)
Suy ra \(\widehat {NAM} = \widehat {EAB} - \widehat {EAN} - \widehat {MAB} = 108^\circ - 36^\circ - 36^\circ = 36^\circ .\)
Do đó \(\widehat {EAN} = \widehat {NAM} = 36^\circ .\)
Vì vậy AN là phân giác của góc EAM.
c) Xét ∆MAB và ∆BAC có:
\(\widehat {AMB} = \widehat {ABC} = 108^\circ \) và \(\widehat {BAC}\) là góc chung
Do đó ∆MAB ᔕ ∆BAC (g.g), suy ra \(\frac{{AB}}{{AC}} = \frac{{BM}}{{CB}}\) hay AB.BC = BM.AC.
Lời giải
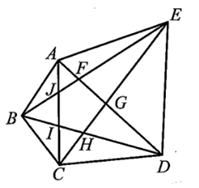
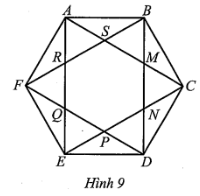
Áp dụng các bất đẳng thức tam giác ta có:
AF + FE > AE (trong tam giác AEF);
AJ + JB > AB (trong tam giác ABJ);
BI + IC > BC (trong tam giác BCI);
CH + HD > CD (trong tam giác CDH);
GE + GD > ED (trong tam giác GDE).
Do đó, ta có:
AF + FE + AJ + JB + BI + IC + CH + HD + GE + GD > AE + AB + BC + CD + ED. (1)
Mặt khác:
(AF + GD) + (JB + FE) + (AJ + IC) + (BI + HD) + (EG + CH) < AD + BE + AC + BD + EC.
Hay AF + FE + AJ + JB + BI + IC + CH + HD + GE + GD < AB + BC + CD + DE + EA. (2)
Từ (1) và (2) suy ra:
AC + AD + BD + BE + EC > AB + BC + CD + DE + EA.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo