Câu hỏi:
25/08/2024 1,098
Cho ngũ giác đều ABCDE, đoạn BE cắt các đoạn AC và AD lần lượt tại M và N. Chứng minh rằng:
a) Các tam giác AEN và CMB là các tam giác cân;
b) AN là phân giác của góc EAM;
c) AB.BC = BM.AC.
Cho ngũ giác đều ABCDE, đoạn BE cắt các đoạn AC và AD lần lượt tại M và N. Chứng minh rằng:
a) Các tam giác AEN và CMB là các tam giác cân;
b) AN là phân giác của góc EAM;
c) AB.BC = BM.AC.
Quảng cáo
Trả lời:
Giải bởi Vietjack
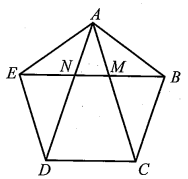
a) Ngũ giác ABCDE là ngũ giác đều nên AB = BC = CD = DE = EA và \(\widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEA} = \widehat {EAB}.\)
Ta cũng có tổng 5 góc của ngũ giác đều ABCDE bằng tổng các góc của ba tam giác ABC, ACD, ADE, tức là bằng 3.180° = 540°.
Do đó: \(\widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEA} = \widehat {EAB} = \frac{{540^\circ }}{5} = 108^\circ .\)
Xét ∆AEB cân tại A (do AB = AE) ta có:
\(\widehat {ABE} = \widehat {AEB} = \frac{{180^\circ - \widehat {EAB}}}{2} = \frac{{180^\circ - 108^\circ }}{2} = 36^\circ .\)
Hay \(\widehat {ABM} = \widehat {AEN} = 36^\circ .\)
Tương tự, đối với ∆EAD cân tại E ta có: \[\widehat {EAD} = \widehat {EDA} = 36^\circ \] hay \[\widehat {EAN} = 36^\circ .\]
Do đó ta có \[\widehat {EAN} = \widehat {NEA} = 36^\circ .\] Suy ra ∆AEN cân tại N.
Tương tự, ta chứng minh được ∆MAB cân tại M (do \(\widehat {MAB} = \widehat {MBA} = 36^\circ )\)
Suy ra \(\widehat {AMB} = 180^\circ - 2\widehat {MAB} = 180^\circ - 2 \cdot 36^\circ = 108^\circ .\)
Mặt khác: \(\widehat {CMB} = 180^\circ - \widehat {AMB} = 180^\circ - 108^\circ = 72^\circ ;\)
\(\widehat {MBC} = \widehat {ABC} - \widehat {ABM} = 108^\circ - 36^\circ = 72^\circ .\)
Suy ra tam giác CMB cân tại C.
b) Ta có: \(\widehat {EAB} = \widehat {EAN} + \widehat {NAM} + \widehat {MAB}\)
Suy ra \(\widehat {NAM} = \widehat {EAB} - \widehat {EAN} - \widehat {MAB} = 108^\circ - 36^\circ - 36^\circ = 36^\circ .\)
Do đó \(\widehat {EAN} = \widehat {NAM} = 36^\circ .\)
Vì vậy AN là phân giác của góc EAM.
c) Xét ∆MAB và ∆BAC có:
\(\widehat {AMB} = \widehat {ABC} = 108^\circ \) và \(\widehat {BAC}\) là góc chung
Do đó ∆MAB ᔕ ∆BAC (g.g), suy ra \(\frac{{AB}}{{AC}} = \frac{{BM}}{{CB}}\) hay AB.BC = BM.AC.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
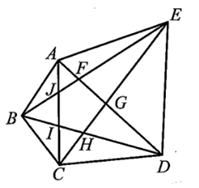
Áp dụng các bất đẳng thức tam giác ta có:
AF + FE > AE (trong tam giác AEF);
AJ + JB > AB (trong tam giác ABJ);
BI + IC > BC (trong tam giác BCI);
CH + HD > CD (trong tam giác CDH);
GE + GD > ED (trong tam giác GDE).
Do đó, ta có:
AF + FE + AJ + JB + BI + IC + CH + HD + GE + GD > AE + AB + BC + CD + ED. (1)
Mặt khác:
(AF + GD) + (JB + FE) + (AJ + IC) + (BI + HD) + (EG + CH) < AD + BE + AC + BD + EC.
Hay AF + FE + AJ + JB + BI + IC + CH + HD + GE + GD < AB + BC + CD + DE + EA. (2)
Từ (1) và (2) suy ra:
AC + AD + BD + BE + EC > AB + BC + CD + DE + EA.
Lời giải
a)
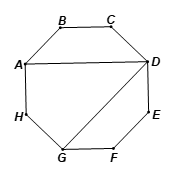
Tổng các góc của đa giác 8 cạnh (bát giác) ABCDEFGH là tổng số đo của ba tứ giác ABCD, ADGH, DEFG, và bằng: 3.360° = 1 080°.
Vậy số đo mỗi góc của đa giác 8 cạnh là: \(\frac{{1\,\,080^\circ }}{8} = 135^\circ .\)
b)
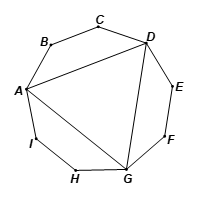
Tổng các góc của đa giác 9 cạnh ABCDEFGHI là tổng số đo của ba tứ giác ABCD, DEFG, GHIA và tam giác ADG, và bằng: 3.360° + 180° = 1 260°.
Vậy số đo mỗi góc của đa giác 9 cạnh là: \(\frac{{1\,\,260^\circ }}{9} = 140^\circ .\)
c)
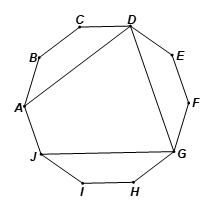
Tổng các góc của đa giác 10 cạnh ABCDEFGHIJ là tổng số đo của bốn tứ giác ABCD, DEFG, GHIJ, JADG và bằng: 4.360° = 1 440°.
Vậy số đo mỗi góc của đa giác 10 cạnh là: \(\frac{{1\,\,440^\circ }}{{10}} = 144^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
-
Chuyên đề 8: Hình học (có đáp án)