Giải SBT Toán 9 Bài 1. Đa giác đều. Hình đa giác đều trong thực tiễn có đáp án
44 người thi tuần này 4.6 321 lượt thi 12 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
19 bài tập Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Lời giải
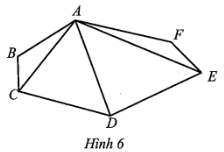
Các đa giác có trong Hình 6 là: tam giác ABC, tam giác ACD, tam giác ADE, tam giác AEF; tứ giác ABCD, tứ giác ACDE, tứ giác ADEF; ngũ giác ABCDE, ngũ giác ACDEF; lục giác ABCDEF.
Lời giải
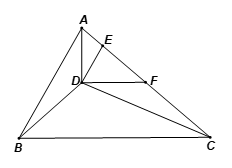
a) Bốn điểm B, D, F, C tạo thành tứ giác BDFC, đây là tứ giác lồi vì tứ giác BDFC nằm về một phía của đường thẳng chứa một cạnh bất kí của tứ giác đó.
Bốn điểm A, B, C, D tạo thành tứ giác ABCD, đây không phải là tứ giác lồi vì tứ giác ABCD nằm về hai phía của đường thẳng AD (hoặc đường thẳng CD).
b) Các điểm A, B, C, D, E tạo thành ngũ giác ABCDE, đây không phải là ngũ giác lồi vì ngũ giác ABCDE nằm về hai phía của đường thẳng CD (hoặc đường thẳng DE).
Lời giải
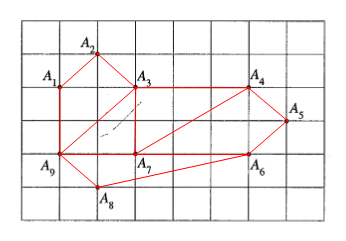
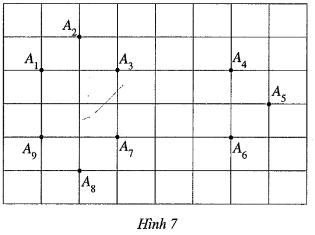
Ta có thể vẽ một số đa giác lồi như sau: tứ giác A1A2A3A9; tứ giác A3A4A7A9; tứ giác A4A5A6A7; ngũ giác A1A2A3A7A9; ngũ giác A3A4A5A6A7; ngũ giác A3A4A5A6A9; lục giác A3A4A5A6A8A9; …
Lời giải
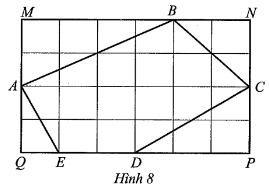
Diện tích của tam giác ABM là: \[\frac{1}{2} \cdot 4 \cdot 2 = 4\,\,{\rm{(c}}{{\rm{m}}^2}).\]
Diện tích của tam giác CBN là: \[\frac{1}{2} \cdot 2 \cdot 2 = 2\,\,{\rm{(c}}{{\rm{m}}^2}).\]
Diện tích của tam giác CPD là: \[\frac{1}{2} \cdot 3 \cdot 2 = 3\,\,{\rm{(c}}{{\rm{m}}^2}).\]
Diện tích của tam giác AQE là: \[\frac{1}{2} \cdot 1 \cdot 2 = 1\,\,{\rm{(c}}{{\rm{m}}^2}).\]
Tổng diện tích các tam giác ABM, CBN, C PD, AQE là:
4 + 2 + 3 + 1 = 10 (đơn vị diện tích).
Diện tích hình chữ nhật MNPQ là: 6.4 = 24 (đơn vị diện tích).
Diện tích ngũ giác ABCDE là hiệu diện tích hình chữ nhật MNPQ và tổng diện tích các tam giác ABM, CBN, C PD, AQE, và bằng:
24 – 10 = 14 (đơn vị diện tích).
Tỉ số diện tích ngũ giác ABCDE và diện tích hình chữ nhật MNPQ là: \(\frac{{14}}{{24}} = \frac{7}{{12}} \approx 0,6.\)
Lời giải
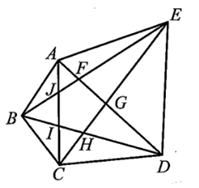
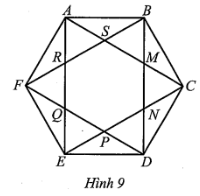
Áp dụng các bất đẳng thức tam giác ta có:
AF + FE > AE (trong tam giác AEF);
AJ + JB > AB (trong tam giác ABJ);
BI + IC > BC (trong tam giác BCI);
CH + HD > CD (trong tam giác CDH);
GE + GD > ED (trong tam giác GDE).
Do đó, ta có:
AF + FE + AJ + JB + BI + IC + CH + HD + GE + GD > AE + AB + BC + CD + ED. (1)
Mặt khác:
(AF + GD) + (JB + FE) + (AJ + IC) + (BI + HD) + (EG + CH) < AD + BE + AC + BD + EC.
Hay AF + FE + AJ + JB + BI + IC + CH + HD + GE + GD < AB + BC + CD + DE + EA. (2)
Từ (1) và (2) suy ra:
AC + AD + BD + BE + EC > AB + BC + CD + DE + EA.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.