Câu hỏi:
25/08/2024 352
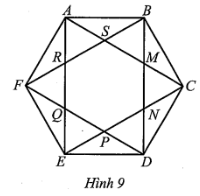
Cho hình chữ nhật MNPQ và ngũ giác ABCDE trên lưới ô vuông như Hình 8, với cạnh của mỗi ô vuông nhỏ là 1 cm. Tính tỉ số diện tích ngũ giác ABCDE và diện tích hình chữ nhật MNPQ (làm tròn đến hàng phần mười).
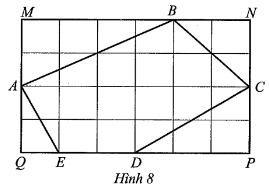
Cho hình chữ nhật MNPQ và ngũ giác ABCDE trên lưới ô vuông như Hình 8, với cạnh của mỗi ô vuông nhỏ là 1 cm. Tính tỉ số diện tích ngũ giác ABCDE và diện tích hình chữ nhật MNPQ (làm tròn đến hàng phần mười).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Diện tích của tam giác ABM là: \[\frac{1}{2} \cdot 4 \cdot 2 = 4\,\,{\rm{(c}}{{\rm{m}}^2}).\]
Diện tích của tam giác CBN là: \[\frac{1}{2} \cdot 2 \cdot 2 = 2\,\,{\rm{(c}}{{\rm{m}}^2}).\]
Diện tích của tam giác CPD là: \[\frac{1}{2} \cdot 3 \cdot 2 = 3\,\,{\rm{(c}}{{\rm{m}}^2}).\]
Diện tích của tam giác AQE là: \[\frac{1}{2} \cdot 1 \cdot 2 = 1\,\,{\rm{(c}}{{\rm{m}}^2}).\]
Tổng diện tích các tam giác ABM, CBN, C PD, AQE là:
4 + 2 + 3 + 1 = 10 (đơn vị diện tích).
Diện tích hình chữ nhật MNPQ là: 6.4 = 24 (đơn vị diện tích).
Diện tích ngũ giác ABCDE là hiệu diện tích hình chữ nhật MNPQ và tổng diện tích các tam giác ABM, CBN, C PD, AQE, và bằng:
24 – 10 = 14 (đơn vị diện tích).
Tỉ số diện tích ngũ giác ABCDE và diện tích hình chữ nhật MNPQ là: \(\frac{{14}}{{24}} = \frac{7}{{12}} \approx 0,6.\)
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
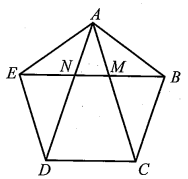
a) Ngũ giác ABCDE là ngũ giác đều nên AB = BC = CD = DE = EA và \(\widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEA} = \widehat {EAB}.\)
Ta cũng có tổng 5 góc của ngũ giác đều ABCDE bằng tổng các góc của ba tam giác ABC, ACD, ADE, tức là bằng 3.180° = 540°.
Do đó: \(\widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEA} = \widehat {EAB} = \frac{{540^\circ }}{5} = 108^\circ .\)
Xét ∆AEB cân tại A (do AB = AE) ta có:
\(\widehat {ABE} = \widehat {AEB} = \frac{{180^\circ - \widehat {EAB}}}{2} = \frac{{180^\circ - 108^\circ }}{2} = 36^\circ .\)
Hay \(\widehat {ABM} = \widehat {AEN} = 36^\circ .\)
Tương tự, đối với ∆EAD cân tại E ta có: \[\widehat {EAD} = \widehat {EDA} = 36^\circ \] hay \[\widehat {EAN} = 36^\circ .\]
Do đó ta có \[\widehat {EAN} = \widehat {NEA} = 36^\circ .\] Suy ra ∆AEN cân tại N.
Tương tự, ta chứng minh được ∆MAB cân tại M (do \(\widehat {MAB} = \widehat {MBA} = 36^\circ )\)
Suy ra \(\widehat {AMB} = 180^\circ - 2\widehat {MAB} = 180^\circ - 2 \cdot 36^\circ = 108^\circ .\)
Mặt khác: \(\widehat {CMB} = 180^\circ - \widehat {AMB} = 180^\circ - 108^\circ = 72^\circ ;\)
\(\widehat {MBC} = \widehat {ABC} - \widehat {ABM} = 108^\circ - 36^\circ = 72^\circ .\)
Suy ra tam giác CMB cân tại C.
b) Ta có: \(\widehat {EAB} = \widehat {EAN} + \widehat {NAM} + \widehat {MAB}\)
Suy ra \(\widehat {NAM} = \widehat {EAB} - \widehat {EAN} - \widehat {MAB} = 108^\circ - 36^\circ - 36^\circ = 36^\circ .\)
Do đó \(\widehat {EAN} = \widehat {NAM} = 36^\circ .\)
Vì vậy AN là phân giác của góc EAM.
c) Xét ∆MAB và ∆BAC có:
\(\widehat {AMB} = \widehat {ABC} = 108^\circ \) và \(\widehat {BAC}\) là góc chung
Do đó ∆MAB ᔕ ∆BAC (g.g), suy ra \(\frac{{AB}}{{AC}} = \frac{{BM}}{{CB}}\) hay AB.BC = BM.AC.
Lời giải
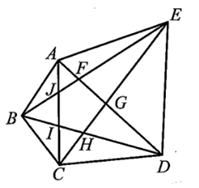
Áp dụng các bất đẳng thức tam giác ta có:
AF + FE > AE (trong tam giác AEF);
AJ + JB > AB (trong tam giác ABJ);
BI + IC > BC (trong tam giác BCI);
CH + HD > CD (trong tam giác CDH);
GE + GD > ED (trong tam giác GDE).
Do đó, ta có:
AF + FE + AJ + JB + BI + IC + CH + HD + GE + GD > AE + AB + BC + CD + ED. (1)
Mặt khác:
(AF + GD) + (JB + FE) + (AJ + IC) + (BI + HD) + (EG + CH) < AD + BE + AC + BD + EC.
Hay AF + FE + AJ + JB + BI + IC + CH + HD + GE + GD < AB + BC + CD + DE + EA. (2)
Từ (1) và (2) suy ra:
AC + AD + BD + BE + EC > AB + BC + CD + DE + EA.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
-
Chuyên đề 8: Hình học (có đáp án)