Câu hỏi:
29/08/2024 2,898
Lúc 7 giờ sáng một xe máy xuất phát từ Thành phố Hồ Chí Minh đi về hướng Biên Hòa với tốc độ trung bình \(40{\rm{\;km}}/\)giờ. Sau đó 15 phút, một ô tô xuất phát từ Biên Hòa đi về hướng Thành phố Hồ Chí Minh với tốc độ trung bình \(60{\rm{\;km}}/\)giờ. Biết rằng Thành phố Hồ Chí Minh cách Biên Hòa \[40{\rm{ km}}.\]
⦁ Gọi \(f\left( t \right) = at + b,\,\,\left( {t \ge 0} \right)\) là hàm số biểu diễn khoảng cách của xe máy so với Thành phố Hồ Chí Minh sau khi đi được \(t\) giờ kể từ lúc 7 giờ 15 phút.
⦁ Gọi \(g\left( t \right) = ct + d,\,\,\left( {0 \le t \le \frac{2}{3}} \right)\) là hàm số biểu diễn khoảng cách của ô tô so với Thành phố Hồ Chí Minh sau khi đi được \(t\) giờ kể từ lúc 7 giờ 15 phút.
a) Tìm các hệ số \(a,\,\,b,\,\,c,\,\,d.\)
b) Hỏi hai xe gặp nhau lúc mấy giờ và nơi gặp nhau cách Thành phố Hồ Chí Minh bao nhiêu ki-lô-mét?
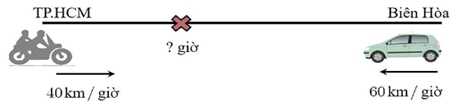
Lúc 7 giờ sáng một xe máy xuất phát từ Thành phố Hồ Chí Minh đi về hướng Biên Hòa với tốc độ trung bình \(40{\rm{\;km}}/\)giờ. Sau đó 15 phút, một ô tô xuất phát từ Biên Hòa đi về hướng Thành phố Hồ Chí Minh với tốc độ trung bình \(60{\rm{\;km}}/\)giờ. Biết rằng Thành phố Hồ Chí Minh cách Biên Hòa \[40{\rm{ km}}.\]
⦁ Gọi \(f\left( t \right) = at + b,\,\,\left( {t \ge 0} \right)\) là hàm số biểu diễn khoảng cách của xe máy so với Thành phố Hồ Chí Minh sau khi đi được \(t\) giờ kể từ lúc 7 giờ 15 phút.
⦁ Gọi \(g\left( t \right) = ct + d,\,\,\left( {0 \le t \le \frac{2}{3}} \right)\) là hàm số biểu diễn khoảng cách của ô tô so với Thành phố Hồ Chí Minh sau khi đi được \(t\) giờ kể từ lúc 7 giờ 15 phút.
a) Tìm các hệ số \(a,\,\,b,\,\,c,\,\,d.\)
b) Hỏi hai xe gặp nhau lúc mấy giờ và nơi gặp nhau cách Thành phố Hồ Chí Minh bao nhiêu ki-lô-mét?
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Đổi 15 phút \( = \frac{1}{4}\) giờ.
Khoảng cách của xe máy so với Thành phố Hồ Chí Minh sau khi đi được \(t\) giờ kể từ lúc 7 giờ 15 phút là: \[f\left( t \right) = 40 \cdot \left( {t + \frac{1}{4}} \right) = 40t + 10,\,\,\left( {t \ge 0} \right).\]
Khoảng cách của ô tô so với Thành phố Hồ Chí Minh sau khi đi được \(t\) giờ kể từ lúc 7 giờ 15 phút là: \[g\left( t \right) = 40 - 60t,\,\,\left( {0 \le t \le \frac{2}{3}} \right).\]
Vậy \(a = 40\,;\,\,b = 10\,;\,\,c = - 60\,;\,\,d = 40.\)
b) Hai xe gặp nhau khi và chỉ khi \(40t + 10 = 40 - 60t\) hay \(100t = 30\) nên \(t = \frac{3}{{10}}\) (giờ).
Đổi \(\frac{3}{{10}}\) giờ \[ = 18\] phút.
Thời điểm hai xe gặp nhau là: 7 giờ 15 phút + 18 phút = 7 giờ 33 phút.
Vị trí gặp cách Thành phố Hồ Chí Minh là: \[40 - 60 \cdot \frac{3}{{10}} = 22\,\,\left( {{\rm{km}}} \right).\]
Vậy hai xe gặp nhau lúc 7 giờ 33 phút và cách Thành phố Hồ Chí Minh 22 km.
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Số tiền anh Tâm phải trả khi thuê pin gói linh hoạt là:
\(189\,\,000 + 374\left( {800 - 400} \right) = 338\,\,600\) (đồng)
Do đó nếu sử dụng gói linh hoạt thì anh Tâm sẽ tiết kiệm được:
\(350\,\,000 - 338\,\,600 = 11400\) (đồng).
Vậy anh Tâm nên sử dụng gói linh hoạt.
Lời giải
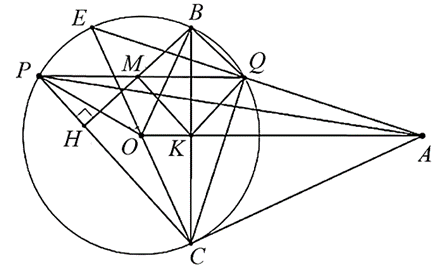
a) Vì \(AB,\,\,AC\) là tiếp tuyến nên \(\widehat {ABO} = \widehat {ACO} = 90^\circ \).
Xét tứ giác \(ABOC\) có
\(\widehat {ABO} + \widehat {ACO} = 90^\circ + 90^\circ = 180^\circ .\)
Mà hai góc này ở vị trí đối diện nên tứ giác \(ABOC\) nội tiếp.
Ta có \(AB = AC\) (tính chất hai tiếp tuyến cắt nhau); \(OB = OC = R\).
Suy ra \(AO\) là đường trung trực của \(BC\) (đpcm).
b) Do \(K\) là trung điểm \(BC,M\) là trung điểm \(BH\) nên \(KM\) là đường trung bình \(\Delta BCH.\)
Suy ra \(KM\,{\rm{//}}\,CH\) nên \(\widehat {QMK} = \widehat {QPC}\) (đồng vị)
Vì \(\Delta OCQ\) cân tại \(O\) \(\left( {OC = OQ} \right)\) nên \(\widehat {OCQ} = \widehat {OQC}.\)
Suy ra \(\widehat {OCQ} = \widehat {OQC} = \frac{{180^\circ - \widehat {COQ}}}{2} = 90^\circ - \frac{{\widehat {COQ}}}{2}.\)
Vì \[AC\] là tiếp tuyến với đường tròn \[\left( O \right)\] tại điểm \[C\] nên \(OC \bot CA\) hay \(\widehat {OCA} = 90^\circ \).
Suy ra \[\widehat {ACQ} = 90^\circ - \widehat {OCQ}\]\[ = 90^\circ - \left( {90^\circ - \frac{{\widehat {COQ}}}{2}} \right) = \frac{{\widehat {COQ}}}{2}.\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\]
Mặt khác nên \[\widehat {QPC} = \frac{{\widehat {COQ}}}{2}.\,\,\,\,\left( 2 \right)\]
Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] suy ra \(\widehat {QCA} = \widehat {QPC}\). Vậy \(\widehat {QMK} = \widehat {QCA}\).
c) Kẻ \(AQ\) cắt \(\left( O \right)\) tại \(E.\)
Xét \(\Delta ACQ\) và \(\Delta AEC\) có \(\widehat {CAE}\) chung; .
Do đó
Suy ra \(\frac{{AC}}{{AE}} = \frac{{AQ}}{{AC}}\) hay AC2 = AE. AQ
Xét \(\Delta ACK\) và \(\Delta AOC\) có \(\widehat {AKC} = \widehat {ACO} = 90^\circ \); \(\widehat {ACK} = \widehat {AOC}\) (cùng phụ \(\widehat {OCK}\,)\).
Do đó .
Suy ra \(\frac{{AC}}{{AK}} = \frac{{AO}}{{AC}}\) hay AC2 = AK. AQ
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(AK \cdot AO = AE \cdot AQ\) hay \(\frac{{AK}}{{AQ}} = \frac{{AE}}{{AO}}\).
Xét \(\Delta AKQ\) và \(\Delta AEO\) có \(\widehat {OAE}\) chung; \(\frac{{AK}}{{AQ}} = \frac{{AE}}{{AO}}\) (chứng minh trên).
Do đó . Suy ra \(\widehat {AKQ} = \widehat {AEO}\).
Chứng minh bổ đề: Cho tứ giác \(ABCD\) có \(\widehat {ACB} = \widehat {ADB}.\) Chứng minh tứ giác \(ABCD\) là tứ giác nội tiếp.
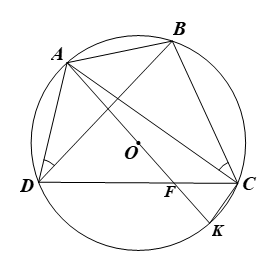
• Giả sử \(\Delta ABC\) có đường tròn ngoại tiếp tâm \(O\) và đường kính \(AK\) nên tứ giác \(ABCK\) nội tiếp, suy ra \(\widehat {ACB} = \widehat {AKB}\) (hai góc nội tiếp cùng chắn cung \(AB).\)
Mà \(\widehat {ACB} = \widehat {ADB}\) (giả thiết) nên \(\widehat {ADB} = \widehat {AKB}.\) \(\left( 6 \right)\)
⦁ Gọi \(F\) là giao điểm của \(AK\) và \(BD,\) \(F\) nằm trong đường tròn \(\left( O \right).\)
Xét \(\Delta AFD\) và \(\Delta BFK\) có: \(\widehat {AFD} = \widehat {BFK}\) (đối đỉnh) và \(\widehat {ADF} = \widehat {BKF}\) (chứng minh trên)
Do đó suy ra \(\frac{{AF}}{{BF}} = \frac{{DF}}{{KF}}\) nên \(\frac{{AF}}{{DF}} = \frac{{BF}}{{KF}}.\)
Xét \(\Delta DFK\) và \(\Delta AFB\) có: \(\frac{{AF}}{{DF}} = \frac{{BF}}{{KF}}\) và \[\widehat {DFK} = \widehat {AFB}\] (đối đỉnh)
Do đó suy ra \(\widehat {FDK} = \widehat {FAB}.\,\,\,\left( 7 \right)\)
⦁ Ta có \(\widehat {ABK}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ABK} = 90^\circ ,\) do đó \(\Delta ABK\) vuông tại \(B,\) suy ra \(\widehat {FAB} + \widehat {AKB} = 90^\circ .\,\,\,\left( 8 \right)\)
Từ \(\left( 6 \right),\,\,\left( 7 \right),\,\,\left( 8 \right)\) suy ra \(\widehat {ADB} + \widehat {FDK} = 90^\circ \) hay \(\widehat {ADK} = 90^\circ .\)
Khi đó \(\Delta ADK\) vuông tại \(D\) nên điểm \(D\) nằm trên đường tròn đường kính \(AK.\)
Suy ra tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) đường kính \(AK.\)
Áp dụng bổ đề trên cho tứ giác \(ACKQ\) có \(\widehat {AKQ} = \widehat {AEO}\) nên tứ giác \(ACKQ\) nội tiếp.
Suy ra \(\widehat {AQC} = \widehat {AKC} = 90^\circ \).
Do \(\widehat {AQC} = 90^\circ \) nên \(\widehat {CQE} = 90^\circ \) nên \(CE\) là đường tròn đường kính của \[\left( O \right)\].
Suy ra ba điểm \(E,\,\,O,\,\,C\) thẳng hàng nên \(\widehat {CPQ} = \widehat {CEQ}\).
Ta có \(\tan \widehat {CPQ} = \tan \widehat {CEQ} = \frac{{AC}}{{EC}} = \frac{{AC}}{{2R}}\).
Do đó \(AC = 2R\tan \widehat {ACQ} = 2R\tan \widehat {CPQ}\) (đpcm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
50 bài tập Một số yếu tố xác suất có lời giải
-
Đề thi tham khảo môn Toán vào 10 tỉnh Quảng Bình năm học 2025-2026
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_TP Hà Nội
-
54 bài tập Hàm số bậc hai và giải bài toán bằng cách lập phương trình có lời giải
-
Đề thi minh họa (Dự thảo) TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đồng Nai
-
Đề thi tham khảo TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Bình Phước