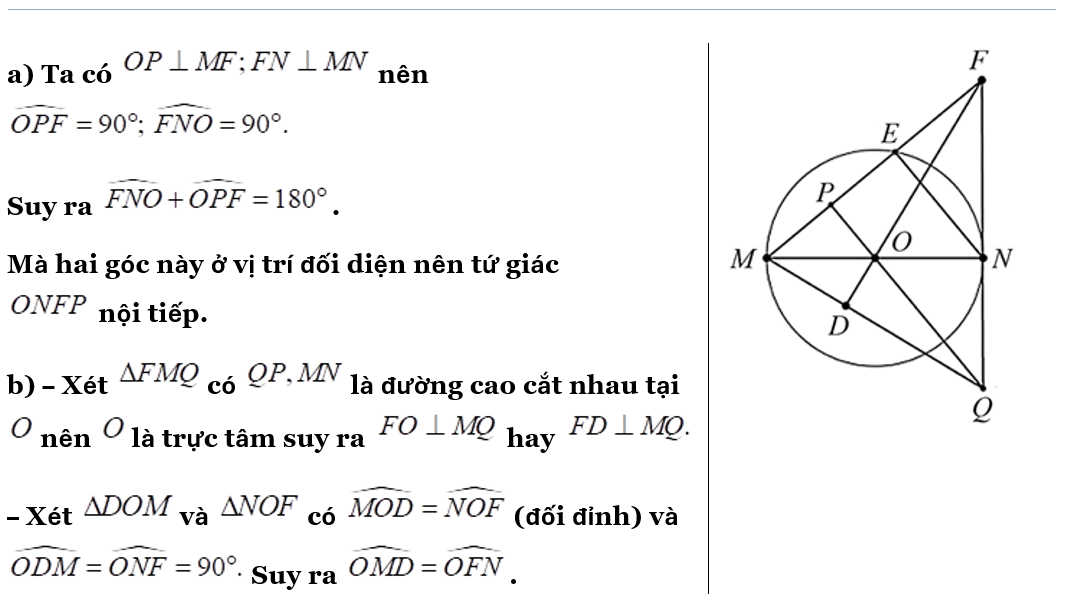
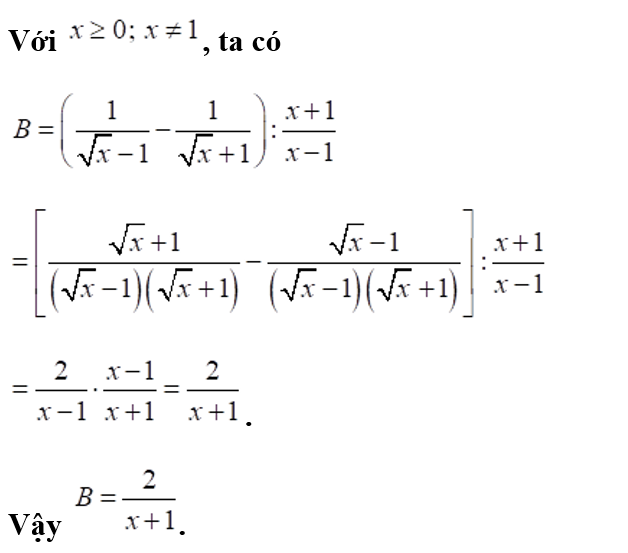Cho đường tròn \(\left( {O\,;R} \right)\) có đường kính \[MN.\] Gọi đường thẳng \(d\) là tiếp tuyến của đường tròn \[\left( O \right)\] tại điểm \(N\). Lấy điểm \(E\) di động trên đường tròn \[\left( O \right)\]\((E\) không trùng với \(M\) và \(N),\) tia \[ME\] cắt đường thẳng \(d\) tại điểm \(F.\) Kẻ \[OP\] vuông góc với \[ME\] tại điểm \(P\), tia \[PO\] cắt đường thẳng \(d\) tại điểm \(Q\), tia \[FO\] cắt \[MQ\] tại điểm \(D.\)
1) Chứng minh tứ giác \[ONFP\] nội tiếp đường tròn.
2) Chứng minh \(MD \cdot DQ = DO \cdot DF.\)
3) Tìm được bao nhiêu điểm \[E\] trên đường tròn \[\left( O \right)\] để tổng \(MF + 4ME\) đạt giá trị nhỏ nhất?
Cho đường tròn \(\left( {O\,;R} \right)\) có đường kính \[MN.\] Gọi đường thẳng \(d\) là tiếp tuyến của đường tròn \[\left( O \right)\] tại điểm \(N\). Lấy điểm \(E\) di động trên đường tròn \[\left( O \right)\]\((E\) không trùng với \(M\) và \(N),\) tia \[ME\] cắt đường thẳng \(d\) tại điểm \(F.\) Kẻ \[OP\] vuông góc với \[ME\] tại điểm \(P\), tia \[PO\] cắt đường thẳng \(d\) tại điểm \(Q\), tia \[FO\] cắt \[MQ\] tại điểm \(D.\)
1) Chứng minh tứ giác \[ONFP\] nội tiếp đường tròn.
2) Chứng minh \(MD \cdot DQ = DO \cdot DF.\)
3) Tìm được bao nhiêu điểm \[E\] trên đường tròn \[\left( O \right)\] để tổng \(MF + 4ME\) đạt giá trị nhỏ nhất?
Quảng cáo
Trả lời:

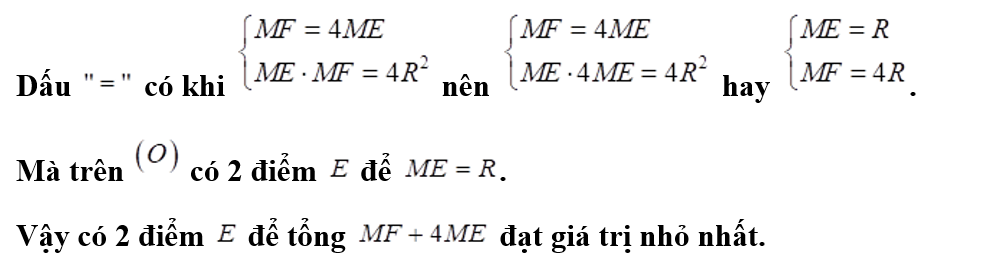
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2
Lời giải
Chọn đáp án A
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.