Câu hỏi:
19/09/2024 1,874
Cho điểm G(1; 2; 3). Viết phương trình mặt phẳng (P) đi qua G và cắt Ox, Oy, Oz lần lượt tại A, B, C sao cho G là trọng tâm của tam giác ABC.
Cho điểm G(1; 2; 3). Viết phương trình mặt phẳng (P) đi qua G và cắt Ox, Oy, Oz lần lượt tại A, B, C sao cho G là trọng tâm của tam giác ABC.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đặt A(a; 0; 0), B(0; b; 0), C(0; 0; c).
Ta có: G(1; 2; 3) là trọng tâm tam giác ABC.
Có \[\left\{ \begin{array}{l}\frac{{a + 0 + 0}}{3} = 1\\\frac{{0 + b + 0}}{3} = 2\\\frac{{0 + 0 + c}}{3} = 3\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 3\\b = 6\\c = 9\end{array} \right.\] ⇒ A(3; 0; 0), B(0; 6; 0), C(0; 0; 9).
Vậy phương trình (P) là: \[\frac{x}{3} + \frac{y}{6} + \frac{z}{9} = 1\] hay 6x + 3y + 2z – 18 = 0.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
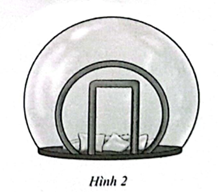
Bề mặt của lều (S): (x – 3)2 + (y – 3)2 + (z – 1)2 = 9 có tâm I(3; 3; 1), bán kính R = 3.
Gọi d là đường thẳng đi qua I và vuông góc với (P): x = 2.
Ta có vectơ chỉ phương của d là \[{\overrightarrow a _d} = \left( {1;0;0} \right)\].
Suy ra d có phương trình tham số \[\left\{ \begin{array}{l}x = 3 + t\\y = 3\\z = 1\end{array} \right.\].
Gọi A(3 + t; 3; 1) là hình chiếu vuông góc của I trên (P). Thay tọa độ điểm A vào phương trình (P): x = 2, ta được (3 + t) – 2 = 0 hay t = −1, suy ra A(2; 3; 1).
Bán kính r1 của đường tròn có cửa lều là:
r1 = \[\sqrt {{R^2} - I{A^2}} = \sqrt {9 - 1} = 2\sqrt 2 \].
Vậy đường tròn cửa lều có tâm A(2; 3; 1), bán kính r1 = \[2\sqrt 2 \].
Gọi d' là đường thẳng đi qua I và vuông góc với (Q): z = 0.
Ta có vectơ chỉ phương của d' là \[{\overrightarrow u _{d'}}\]= (0; 0; 1)
Suy ra d' có phương trình tham số: \[\left\{ \begin{array}{l}x = 3\\y = 3\\z = 1 + t.\end{array} \right.\]
Gọi B(3; 3; 1 + t) là hình chiếu vuông góc của I trên (Q). Thay tọa độ của điểm B vào phương trình (Q): z = 0 ta được 1 + t = 0, suy ra t = −1, suy ra B(3; 3; 0).
Bán kính r1 của đường tròn sàn lều là: r2 = \[\sqrt {{R^2} - I{B^2}} = \sqrt {9 - 1} = 2\sqrt 2 \].
Vậy đường tròn sàn lều có tâm B(3; 3; 0), bán kính r2 = \[2\sqrt 2 \].
Lời giải
Mặt cầu (S) có phương trình x2 + y2 + z2 – 2ax – 2by – 2cz + d = 0 (1).
Thay tọa độ bốn đỉnh của tứ diện vào (1), ta được:
\[\left\{ \begin{array}{l}{2^2} + {0^2} + {0^2} - 2a.2 - 2b.0 - 2c.0 + d = 0\\{0^2} + {4^2} + {0^2} - 2a.0 - 2b.4 - 2c.0 + d = 0\\{0^2} + {0^2} + {4^2} - 2a.0 - 2b.0 - 2c.4 + d = 0\\{0^2} + {0^2} + {0^2} - 2a.0 - 2b.0 - 2c.0 + d = 0\end{array} \right.\]
⇔ \[\left\{ \begin{array}{l}4 - 4a + d = 0\\16 - 8b + d = 0\\16 - 8c + d = 0\\d = 0\end{array} \right.\]
⇔ \[\left\{ \begin{array}{l}a = 1\\b = 2\\c = 2\\d = 0\end{array} \right.\].
Vậy phương trình của (S) là: x2 + y2 + z2 – 2x – 4y – 4z = 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận