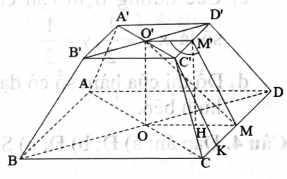
Một toà nhà có dạng hình chóp cụt tứ giác đều với cạnh đáy lớn là 14 m, cạnh đáy nhỏ là 8 m, cạnh bên là 5 m. Xét góc nhị diện có cạnh chứa cạnh đáy nhỏ, một mặt nhị diện chứa đáy nhỏ và mặt nhị diện còn lại chứa mặt bên của hình chóp cụt đều. Số đo góc nhị diện đó bằng \({{\rm{n}}^o }\) (làm tròn kết quả đến hàng đơn vị) với n là số tự nhiên. Giá trị của n là bao nhiêu?

Xem lời giải

Câu hỏi trong đề: (2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 3) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp số: 139.

\({\rm{MK}} = \frac{{{{\rm{C}}^\prime }{{\rm{D}}^\prime }}}{2} = 4(\;{\rm{m}})\)\({\rm{CK}} = {\rm{MC}} - {\rm{MK}} = 7 - 4 = 3(\;{\rm{m}}).\)

\({{\rm{C}}^\prime }{{\rm{K}}^2} = {\rm{C}}{{\rm{C}}^{\prime 2}} - {\rm{C}}{{\rm{K}}^2} = {5^2} - {3^2} = 16\),

\({{\rm{C}}^\prime }{\rm{K}} = 4(\;{\rm{m}}).\)

\({\rm{M}}{{\rm{M}}^\prime } = {{\rm{C}}^\prime }{\rm{K}} = 4(\;{\rm{m}}).\)

\({\rm{MH}} = {\rm{OM}} - {\rm{OH}} = 7 - 4 = 3(\;{\rm{m}}).\)

\(\cos \widehat {{\rm{M}}{{\rm{M}}^\prime }{{\rm{O}}^\prime }} = - \cos \widehat {{\rm{HM}}{{\rm{M}}^\prime }} = - \frac{{{\rm{HM}}}}{{{\rm{M}}{{\rm{M}}^\prime }}} = - \frac{3}{4}\),

\(\widehat {{\rm{M}}{{\rm{M}}^\prime }{{\rm{O}}^\prime }} \approx {139^o }.\)

Một toà nhà có dạng hình chóp cụt tứ giác đều với cạnh đáy lớn là 14 m, cạnh đáy nhỏ là 8 m, cạnh bên là 5 m. Xét góc nhị diện có cạnh chứa cạnh đáy nhỏ, (ảnh 1)

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Hoạ sĩ thiết kế một chiếc mũ xe máy có dạng khối tròn xoay, mặt cắt đứng chứa tâm của khối tròn xoay có dạng một cung tròn bán kính 20 cm, với độ dài dây cung là 32 cm (hình bên). Thể tích của khối tròn xoay này là bao nhiêu \({\rm{d}}{{\rm{m}}^3}\) ? (Làm tròn kết quả đến hàng đơn vị)

Xem đáp án

Lời giải

Đáp số: 30.

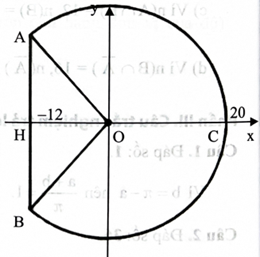
Hoạ sĩ thiết kế một chiếc mũ xe máy có dạng khối tròn xoay, mặt cắt đứng chứa tâm của khối tròn xoay có dạng một cung tròn bán kính 20 cm, (ảnh 2)

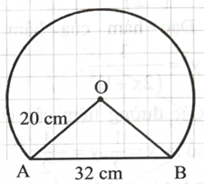
Chọn hệ trục toạ độ như hình vẽ, đơn vị của mỗi trục là 1 cm. Đường tròn chứa cung tròn lớn ACB có phương trình \({{\rm{x}}^2} + {{\rm{y}}^2} = 400.\)

\({\rm{AH}} = {\rm{BH}} = 16\), suy ra \({\rm{OH}} = 12\) và \({\rm{H}}( - 12;0).\)

Suy ra những điểm ( \(x\); y) thuộc cung nhỏ AC thoả mãn \({\rm{x}} \in [ - 12;20],{\rm{y}} = \sqrt {400 - {{\rm{x}}^2}} .\)

Hàm số \({\rm{f}}({\rm{x}}) = \sqrt {400 - {{\rm{x}}^2}} ,{\rm{x}} \in [ - 12;20]\) có đồ thị là cung nhỏ AC. Thể tích của chiếc mũ là

\({\rm{V}} = \pi \int_{ - 12}^{20} {{{\left( {\sqrt {400 - {{\rm{x}}^2}} } \right)}^2}} {\rm{dx}} = \pi \int_{ - 12}^{20} {\left( {400 - {{\rm{x}}^2}} \right)} {\rm{dx}}\)

\({\rm{V}} = \left. {\pi \left( {400{\rm{x}} - \frac{{{{\rm{x}}^3}}}{3}} \right)} \right|_{ - 12}^{20} = \pi \left( {400.20 - \frac{{{{20}^3}}}{3}} \right) - \pi \left[ {400.( - 12) - \frac{{{{( - 12)}^3}}}{3}} \right]\)

\( = \frac{{16000\pi }}{3} + 4224\pi = \frac{{28672\pi }}{3} \approx 30025\left( {\;{\rm{c}}{{\rm{m}}^3}} \right).\)

\( \approx 30\left( {{\rm{d}}{{\rm{m}}^3}} \right)\)

Câu 2

Một phân xưởng sản xuất bóng đèn có tỉ lệ bóng đạt chuẩn là 95%. Để hạn chế số lượng bóng không đạt chuẩn được bán ra thị trường, người ta lắp đặt một thiết bị kiểm tra chất lượng tự động S. Nếu một bóng đèn không đạt chuẩn, thiết bị S sẽ loại bỏ nó với xác suất 0,99. Khi kiểm tra lại các bóng đèn bị loại, người ta nhận thấy có 10% số đó là bóng đạt chuẩn. Chọn ngẫu nhiên 1 bóng đèn do phân xưởng đó sản xuất. Xác suất bóng đèn được chọn đạt chuẩn biết rằng nó không bị thiết bị S loại bỏ bằng \(\frac{{\rm{a}}}{{\rm{b}}}\) với a, b là số nguyên dương và \({\rm{b}} < 2000.\) Giá trị của biểu thức \({\rm{a}} + {\rm{b}}\) là bao nhiêu?

Xem đáp án

Lời giải

Đáp số: 3779.

Chọn ngẫu nhiên 1 bóng đèn do phân xưởng sản xuất.

Gọi C là biến cố bóng đèn đó đạt chuẩn và L là biến cố bóng đèn đó bị thiết bị S loại.

Ta có \({\rm{P}}({\rm{C}}) = 0,95;{\rm{P}}({\rm{L}}\mid \overline {\rm{C}} ) = 0,99;{\rm{P}}({\rm{C}}\mid {\rm{L}}) = 0,1.\)

Suy ra \(P(L) = \frac{{P(L\mid \bar C)P(\overline {\rm{C}} )}}{{{\rm{P}}(\overline {\rm{C}} \mid {\rm{L}})}} = \frac{{0,99 \cdot 0,05}}{{1 - 0,1}} = \frac{{11}}{{200}}\)

và \({\rm{P}}({\rm{CL}}) = {\rm{P}}({\rm{C}}\mid {\rm{L}}) \cdot {\rm{P}}({\rm{L}}) = 0,1 \cdot \frac{{11}}{{200}} = \frac{{11}}{{2000}}.\)

Xác suất bóng đèn được chọn đạt chuẩn biết rằng nó không bị thiết bị S loại là \({\rm{P}}({\rm{C}}\mid \overline {\rm{L}} ) = \frac{{{\rm{P}}({\rm{C}}\overline {\rm{L}} )}}{{{\rm{P}}(\overline {\rm{L}} )}} = \frac{{{\rm{P}}({\rm{C}}) - {\rm{P}}({\rm{CL}})}}{{1 - {\rm{P}}({\rm{L}})}} = \frac{{1889}}{{1890}}.\) Suy \({\rm{raa}} + {\rm{b}} = 3779.\)

Câu 3