Đường cong trong hình dưới là đồ thị của hàm số nào trong bốn hàm số sau đây?
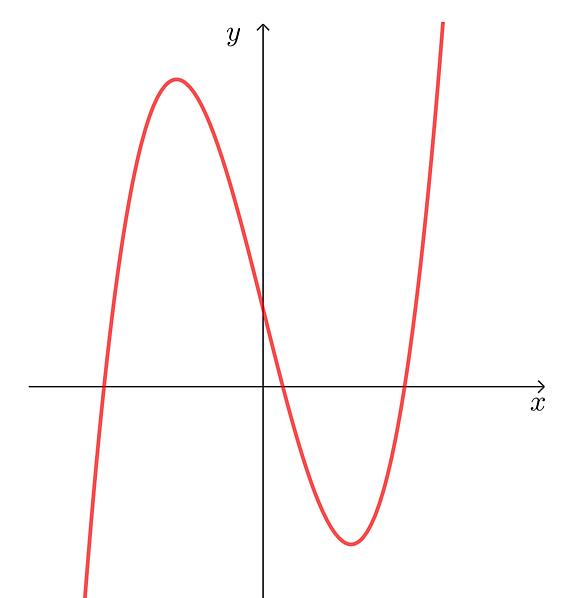
Đường cong trong hình dưới là đồ thị của hàm số nào trong bốn hàm số sau đây?

Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 12 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: A
Dựa vào đồ thị hàm số ta thấy:
Đồ thị hàm số cắt trục tung tại điểm có tọa độ \(\left( {0;d} \right)\) với \(d > 0\) nên ta loại đáp án C.
\(\mathop {\lim }\limits_{x \to + \infty } y = + \infty \), suy ra hệ số \(a > 0\) nên ta loại đáp án D.
Mặt khác hàm số đạt cực trị tại hai điểm \({x_1},\,{x_2}\), dựa vào hình vẽ ta thấy \({x_1},\,{x_2}\) trái dấu nên đáp án ta loại đáp án B và chọn A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là: D
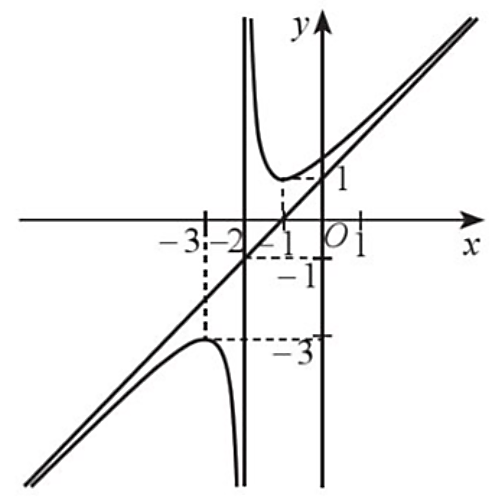
Đồ thị hàm số đã cho nhận giao điểm của hai đường tiệm cận làm tâm đối xứng.
Giao điểm này có tọa độ là \(\left( { - 1;\,0} \right)\).
Câu 2
Lời giải
Đáp án đúng là: C
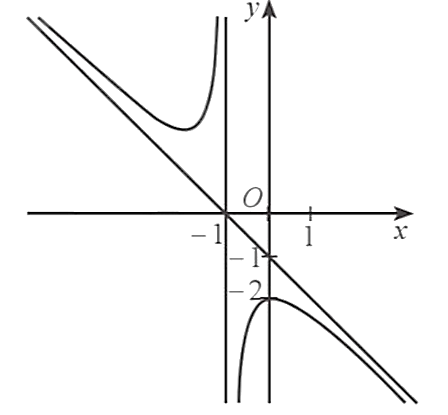
Ta có \[\mathop {\lim }\limits_{x \to + \infty } \left[ {y - \left( {2x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \left( { - \frac{3}{{x + 1}}} \right) = 0\]; \[\mathop {\lim }\limits_{x \to - \infty } \left[ {y - \left( {2x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } \left( { - \frac{3}{{x + 1}}} \right) = 0\].
Do đó, đường thẳng \(y = 2x + 1\) là tiệm cận xiên của đồ thị hàm số đã cho.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.