II. Thông hiểu
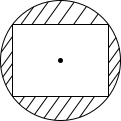
Đường tròn nội tiếp hình vuông cạnh \[a\] có bán kính là
A. \(a\sqrt 2 \).
B. \(\frac{{a\sqrt 2 }}{2}\).
C. \(\frac{a}{2}\).
D. \(\frac{{a\sqrt 3 }}{2}\).
Quảng cáo
Trả lời:
Đáp án đúng là: C
Gọi \[O\] là tâm của hình vuông \[ABCD\].
Gọi \[E;{\rm{ }}F;{\rm{ }}K;{\rm{ }}G\] lần lượt là trung điểm của \[AD,{\rm{ }}DC,{\rm{ }}BC,{\rm{ }}AB\].
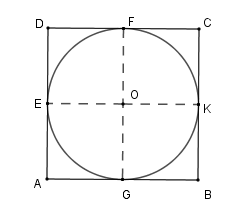
Khi đó ta có \[OE = OF = OK = OG = \;\frac{a}{2}\] hay \[O\] là tâm đường tròn nội tiếp hình vuông \[ABCD\].
Vậy bán kính đường tròn nội tiếp hình vuông là \(R = \frac{a}{2}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(30^\circ \).
B. \(45^\circ \).
C. \(60^\circ \).
D. \(15^\circ \).
Lời giải
Đáp án đúng là: D
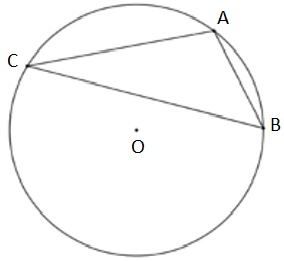
Vì \[AC\] bằng cạnh của hình vuông nội tiếp \[\left( O \right)\] nên số đo cung \[AC = 90^\circ \].
Vì \[BC\] bằng cạnh của tam giác đều nội tiếp \[\left( O \right)\] nên số đo cung \[BC = 120^\circ \].
Từ đó suy ra số đo cung \[AB\] bằng \[120^\circ --90^\circ = 30^\circ \].
Vì góc \[ACB\] là góc nội tiếp chắn cung \[AB\] nên \(\widehat {ACB} = \frac{{30^\circ }}{2} = 15^\circ \).
Vậy \(\widehat {ACB} = 15^\circ \).
Câu 2
A. \(\frac{{a\sqrt 3 }}{6}\).
B. \(\frac{{a\sqrt 3 }}{3}\).
C. \(\frac{a}{6}\).
D. \(\frac{a}{3}\).
Lời giải
Đáp án đúng là: B
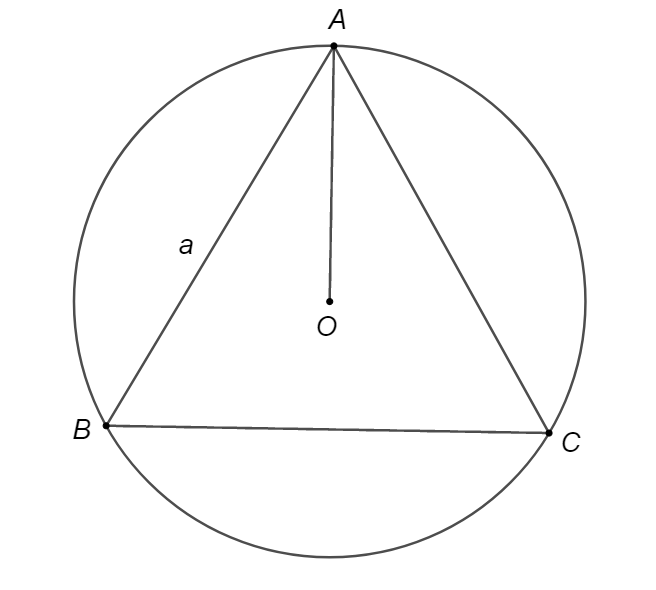
Đường tròn ngoại tiếp tam giác đều cạnh
\(a\) có bán kính bằng \(\frac{{a\sqrt 3 }}{3}\).Câu 3
A. 26 cm.
B. 13 cm.
C. \(\frac{{13}}{2}\,\,{\rm{cm}}\).
D. 6 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[16,12{\rm{ c}}{{\rm{m}}^{\rm{2}}}{\rm{.}}\]
B. \[16,84{\rm{ c}}{{\rm{m}}^{\rm{2}}}{\rm{.}}\]
C. \[{\rm{24,15 c}}{{\rm{m}}^{\rm{2}}}{\rm{.}}\]
D. \[{\rm{24,05 c}}{{\rm{m}}^{\rm{2}}}{\rm{.}}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(BD = \frac{{BC + AB - AC}}{2}\).
B. \(BC = \frac{{BD + AB - AC}}{2}\).
C. \(BD = \frac{{BC + AB + AC}}{2}\).
D. \(BD = \frac{{BC - AB + AC}}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.