Tam giác \(ABC\) vuông tại \(A\) có \(AB = 4\,\,{\rm{cm}}\), \(AB = 3\,\,{\rm{cm}}\) nội tiếp nửa đường tròn tâm \(O\) đường kính \(BC\). Khi quay nửa hình tròn tâm \(O\) bán kính \(R\) quanh đường kính \(BC\) cố định ta thu được một hình cầu có bán kính là
A. \[2,5{\rm{\;cm}}.\]
B. \[3{\rm{\;cm}}.\]
C. \[4{\rm{\;cm}}.\]
D. \[5{\rm{\;cm}}.\]
Quảng cáo
Trả lời:
Đáp án đúng là: A
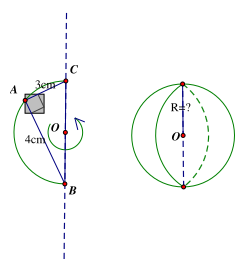
Khi quay nửa hình tròn tâm \(O\) quanh đường kính \(BC\) cố định ta thu được một hình cầu có đường kính \(BC\) và bán kính là \(R = \frac{{BC}}{2}\)
Áp dụng định lý Pythagore cho tam giác \(ABC\) vuông tại \(A,\) ta có:
\(B{C^2} = A{C^2} + A{B^2} = {3^2} + {4^2} = 25\)
Suy ra \(BC = \sqrt {25} = 5\) (do \(BC > 0).\)
Do đó \(R = \frac{{BC}}{2} = \frac{5}{2} = 2,5\) cm.
Vậy ta chọn phương án A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[3{\rm{\;cm}}.\]
B. \[3,5{\rm{\;cm}}.\]
C. \[2,5{\rm{\;cm}}.\]
D. \[4{\rm{\;cm}}.\]
Lời giải
Đáp án đúng là: A
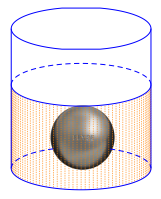
Ta thấy thể tích của viên bi bị bạn An đã bỏ vào lọ thủy tinh bằng thể tích của phần nước trong lọ thủy tinh dâng lên thêm \[2,25{\rm{\;cm}}.\]
Bán kính của lọ thủy tinh là: \[r = \frac{8}{2} = 4{\rm{\;(cm)}}{\rm{.}}\]
Thể tích phần nước trong lọ thủy tinh dâng lên thêm \[2,25{\rm{\;cm}}\] là:
\[V = \pi {r^2}h = \pi \cdot {4^2} \cdot 2,25 = 36\pi {\rm{\;(c}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\]
Suy ra thể tích của viên bi bị bạn An đã bỏ vào lọ thủy tinh bằng \[36\pi {\rm{\;(c}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\]
Gọi \(R{\rm{\;(cm)}}\) là bán kính của viên bi đặc hình cầu.
Thể tích của viên bi đó là: \(V = \frac{4}{3}\pi {R^3}{\rm{\;(c}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\)
Khi đó, ta có: \[\frac{4}{3}\pi {R^3} = 36\pi \]
Suy ra \[{R^3} = \frac{{36\pi }}{{\frac{4}{3}\pi }} = 27\] nên \[R = \sqrt[3]{{27}} = 3{\rm{\;(cm)}}{\rm{.}}\]
Do đó bán kính của viên bi bị bạn An đã bỏ vào lọ thủy tinh là \[3{\rm{\;cm}}.\]
Vậy ta chọn phương án A.
Câu 2
A. \[140\] lít.
B. \[139\] lít.
C. \[138\] lít.
D. \[141\] lít.
Lời giải
Đáp án đúng là: B
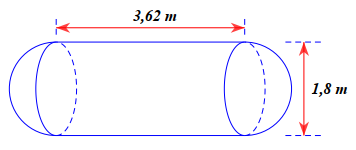
Dung tích của bể chứa là:
\[V = \frac{4}{3}\pi {R^3} \approx \frac{4}{3} \cdot 3,14 \cdot {6^3} = 904,320{\rm{\;(}}{{\rm{m}}^3}{\rm{)}} = 904\,\,320{\rm{\;(d}}{{\rm{m}}^3}{\rm{)}} = 904\,\,320\,\,(l).\]
Số lít nước người ta đã dự tính mức bình quân mỗi người dùng trong một ngày là:
\[904\,\,320:6\,\,520 \approx 139{\rm{\;(}}l{\rm{)}}{\rm{.}}\]
Do đó người ta đã dự tính mức bình quân mỗi người dùng \[139\] lít nước trong một ngày.
Vậy ta chọn phương án B.
Câu 3
A. \[9198,1{\rm{\;c}}{{\rm{m}}^3}.\]
B. \[1\,\,149,7{\rm{\;c}}{{\rm{m}}^3}.\]
C. \[9198,0{\rm{\;c}}{{\rm{m}}^3}.\]
D. \[1\,\,149,8{\rm{\;c}}{{\rm{m}}^3}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[191,54{\rm{\;mm}}.\]
B. \[95,77{\rm{\;mm}}.\]
C. \[182,65{\rm{\;mm}}.\]
D. \[150,68{\rm{\;mm}}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[4,5042\pi {\rm{\;}}{{\rm{m}}^3}.\]
B. \[0,972\pi {\rm{\;}}{{\rm{m}}^3}.\]
C. \[3,9{\rm{\;}}{{\rm{m}}^3}.\]
D. \[3,9042\pi {\rm{\;}}{{\rm{m}}^3}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. hình vuông.
B. hình chữ nhật.
C. hình tam giác.
D. hình tròn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[225{\rm{\;c}}{{\rm{m}}^2}.\]
B. \[225\pi {\rm{\;c}}{{\rm{m}}^2}.\]
C. \[900{\rm{\;c}}{{\rm{m}}^2}.\]
D. \[900\pi {\rm{\;c}}{{\rm{m}}^2}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.