Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: D
Ta có: ![]()
![]()
![]()
![]()
Vậy chọn đáp án D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi ![]() là số học sinh của lớp 9A,
là số học sinh của lớp 9A, ![]() là số học sinh của lớp 9B
là số học sinh của lớp 9B ![]() .
.
Theo đề bài, tổng số học sinh hai lớp là ![]() học sinh nên ta có phương trình
học sinh nên ta có phương trình ![]()
Lớp 9A góp được số giấy báo cũ là ![]() .
.
Lớp 9B góp được số giấy báo cũ là ![]() .
.
Mà lớp 9B góp nhiều hơn lớp 9A ![]() giấy báo cũ nên ta có phương trình:
giấy báo cũ nên ta có phương trình:
![]() suy ra
suy ra ![]() hay
hay ![]() .
.
Từ (1) và (2) ta có hệ phương trình: 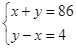 .
.
Cộng theo vế hai phương trình ta được ![]() , suy ra
, suy ra ![]() (TM).
(TM).
Thay ![]() vào phương trình (1), ta được
vào phương trình (1), ta được ![]() , suy ra
, suy ra ![]() (TM).
(TM).
Vậy lớp 9A có ![]() học sinh, lớp 9B có
học sinh, lớp 9B có ![]() học sinh.
học sinh.
Lời giải
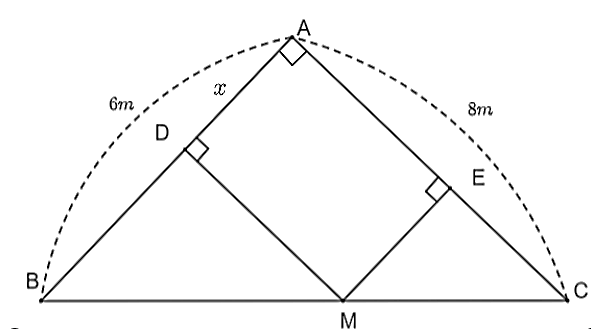
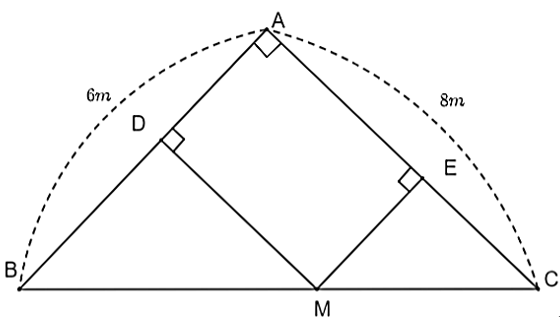
Đặt \[AD = x\,\,\left( {x > 0} \right)\].
Ta có tứ giác \[ADME\] có \[\widehat {ADE} = \widehat {DAE} = \widehat {AED} = 90^\circ \] nên \[ADME\] là hình chữ nhật. Do đó, \[AD = EM = x.\]
Xét \[\Delta ABC\] và \[\Delta ECM\] có:
\(\widehat A = \widehat {MEC} = 90^\circ \,;\,\,\widehat C\) chung.
Do đó (g.g)
Suy ra \[\frac{{EM}}{{AB}} = \frac{{CE}}{{CA}}\] hay \[\frac{x}{6} = \frac{{CE}}{8}\] suy ra \[CE = \frac{4}{3}x\].
Ta có \[AE = AC - EC = 8 - \frac{4}{3}x\].
Diện tích hình chữ nhật \[ADME\] là:
\[{S_{ADME}} = AD.AE = x\left( {8 - \frac{4}{3}x} \right)\].
Ta có: \[x\left( {8 - \frac{4}{3}x} \right) = - \frac{4}{3}{x^2} + 8x = - \frac{4}{3}\left( {{x^2} - 6x} \right)\]
\[ = - \frac{4}{3}\left( {{x^2} - 6x + 9} \right) + 12\]
\[ = - \frac{4}{3}{\left( {x - 3} \right)^2} + 12\].
Vì \[{\left( {x - 3} \right)^2} \ge 0\] với mọi \(x \in \mathbb{R}\) nên \[ - \frac{4}{3}{\left( {x - 3} \right)^2} \le 0\] với mọi \(x \in \mathbb{R}\).
Do đó \[ - \frac{4}{3}{\left( {x - 3} \right)^2} + 12 \le 12\] với mọi \(x \in \mathbb{R}\).
Dấu “=” xảy ra khi \[x - 3 = 0\] khi \[x = 3.\]
Khi đó \[D\] là trung điểm của \[AB\].
Suy ra \[M\] là trung điểm của \[BC\].
Do đó, diện tích lớn nhất của \[ADME\] bằng \[{\rm{12 }}{{\rm{m}}^{\rm{2}}}\] khi \[M\] là trung điểm của \[BC\].
Vậy diện tích ao cá lớn nhất mà người đó có thể đào là \[{\rm{12 }}{{\rm{m}}^{\rm{2}}}\] khi \[M\] là trung điểm của \[BC\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.