Giải phương trình
\(\frac{{x - 1}}{{x + 1}} - \frac{{x + 1}}{{x - 1}} = \frac{8}{{{x^2} - 1}}.\)
\(\frac{{x - 1}}{{x + 1}} - \frac{{x + 1}}{{x - 1}} = \frac{8}{{{x^2} - 1}}.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Điều kiện xác định: \(x \ne 1\) và \(x \ne - 1\).
Ta có: \(\frac{{x - 1}}{{x + 1}} - \frac{{x + 1}}{{x - 1}} = \frac{8}{{{x^2} - 1}}\)
\(\frac{{x - 1}}{{x + 1}} - \frac{{x + 1}}{{x - 1}} = \frac{8}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\)
\(\frac{{{{\left( {x - 1} \right)}^2} - {{\left( {x + 1} \right)}^2}}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} = \frac{8}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\)
\({\left( {x - 1} \right)^2} - {\left( {x + 1} \right)^2} = 8\)
\(\left( {x - 1 + x + 1} \right)\left( {x - 1 - x - 1} \right) = 8\)
\(2x.\left( { - 2} \right) = 8\)
\( - 4x = 8\)
\(x = - 2\) (thỏa mãn).
Vậy nghiệm của phương trình là \(x = - 2\).Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét tam giác 
vuông tại 
, ta có:
Xét tam giác 
vuông tại , ta có:
Do 
nên 
Hay 
.
Suy ra 
(m).
Vậy tháp Eiffel có độ cao khoảng 
(m).
Lời giải
Chiều dài của đáy bể là 
Diện tích đáy của bể là 
Chiều cao của bể là: 
.
Diện tích xung quanh của bể là: 
Diện tích cần xây bằng tổng diện tích xung quanh và diện tích đáy của bể, và bằng:
Do 
là chiều rộng của bể nên 
, áp dụng bất đẳng thức Cauchy, ta có:
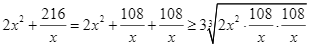
Suy ra 
Dấu “=” xảy ra khi 
hay 
, tức là 
Vậy muốn diện tích cần xây là tiết kiệm chi phí nhất thì 
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập