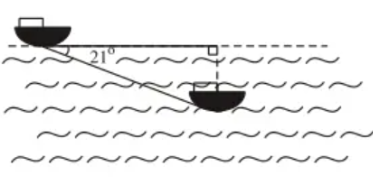
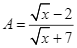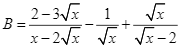Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Ta có: 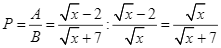 .
.
Ta có 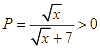 với mọi
với mọi ![]() nên
nên ![]() luôn xác định.
luôn xác định.
Để ![]() suy ra
suy ra ![]() . Mà
. Mà 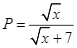 nên
nên 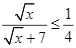 .
.
Giải bất phương trình: 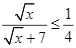
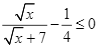
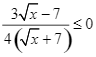
Do ![]() nên
nên ![]() , suy ra
, suy ra 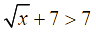 và
và 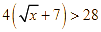 .
.
Suy ra ![]() nên
nên ![]() , suy ra
, suy ra ![]() .
.
Kết hợp điều kiện, suy ra ![]() và
và ![]()
Mà ![]() nên
nên ![]() .
.
Vậy ![]() là các giá trị nguyên cần tìm để
là các giá trị nguyên cần tìm để ![]() .
.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
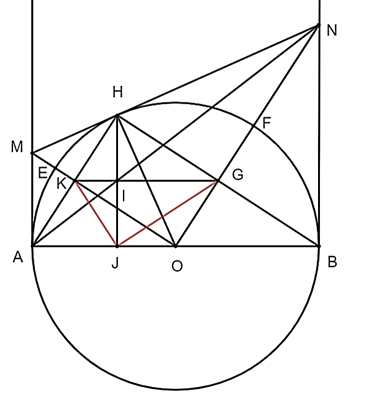
a) Theo tính chất hai tiếp tuyến cắt nhau, ta có: \[OM\] là tia phân giác của \[\widehat {AOH}\], \[ON\] là tia phân giác của \[\widehat {BOH}\].
Mà \[\widehat {AOH}\] và \[\widehat {BOH}\] là hai góc kề bù nên \[\widehat {MON} = 90^\circ \].
Suy ra tam giác \[OMN\] vuông tại \[O\] có \[OM \bot ON\].
Xét \[\Delta HOM\] và \[\Delta HNO\], có:
\[\widehat {MHO} = \widehat {OHN} = 90^\circ \] (gt)
\[\widehat {HMO} = \widehat {HON}\] (cùng phụ với \[\widehat {MOH}\])
Do đó, (g.g) nên \[\frac{{HO}}{{HN}} = \frac{{HM}}{{HO}}\].
Suy ra \[O{H^2} = HM.HN\].
Theo tính chất của hai tiếp tuyến cắt nhau, ta có: \[AM = HM\] và \[HN = BN\].
Do đó, \[O{H^2} = HM.HN = AM.BN\] suy ra \[{R^2} = AM.BN\]. (1)
Mà ta có: \[AB = 2R\] suy ra \[A{B^2} = 4{R^2}\] do đó \[{R^2} = \frac{{A{B^2}}}{4}.\] (2)
Từ (1) và (2) suy ra \[AM.BN = \frac{{A{B^2}}}{4}\] (đpcm).
b) Vì \[AM \bot AB,BN \bot AB\] nên \[AM\parallel BN\].
Xét tứ giác \[ABNM\] có \[AM\parallel BN\] và \[\widehat {BAM} = 90^\circ \,\,\left( {AM \bot AB} \right).\]
Do đó, \[ABNM\] là hình thang vuông.
Ta có: \[{S_{MON}} = \frac{1}{2}OH.MN \ge \frac{1}{2}OH.AB\] (vì \[ABNM\] là hình thang vuông tại \(A\) và \(B\) nên\(MN \ge AB\)).
Dấu “=” xảy ra khi và chỉ khi \[MN = AB\]. Khi đó, \[ABNM\] là hình chữ nhật và \[H\] là điểm chính giữa cung \[AB\] suy ra \[NM\parallel AB\].
Ta có \[OH \bot AO,OH \bot MN\] nên \[AOHM\] là hình chữ nhật, mà \[OA = OH = R\] suy ra \[AOHM\] là hình vuông.
Tương tự, ta có: \[OBNH\]là hình vuông.
Do đó, \[AM = BN = OH = \frac{{AB}}{2}\].
Vậy \[{S_{MON}}\] nhỏ nhất khi \[AM = BN = \frac{{AB}}{2}.\]
c) \(\Delta OAH\) cân tại \(O\) và có \(OK\) là phân giác của \(\widehat {AOH}\) (\(K \in OM\)).
Suy ra \(OK\) cũng là đường trung tuyến của \(\Delta OAH\).
Do đó, \(K\) là trung điểm của \(AH\).
Ta có: \(ON\) là phân giác của \(\widehat {BOH}\) (tính chất hai tiếp tuyến cắt nhau).
Xét \(\Delta OBH\) cân tại \(O\) có \(OG\) là phân giác của \(\widehat {BOH}\) (\(G \in ON\)).
Suy ra \(OG\) cũng là đường trung tuyến của \(\Delta OBH\).
Do đó, \(G\) là trung điểm của \(BH\).
Xét \(\Delta HAJ\) vuông tại \(J\) có \(JK = \frac{1}{2}HA\) (đường trung tuyến ứng với cạnh huyền).
\(\Delta HBJ\) vuông tại \(J\) có \(JG = \frac{1}{2}HB\) (đường trung tuyến ứng với cạnh huyền).
\(\Delta HAB\) vuông tại \(H\) có \(A{H^2} + H{B^2} = A{B^2} = 4{R^2}\) (định lí Pythagore).
Do đó, \[J{G^2} + J{K^2} = \frac{1}{4}H{A^2} + \frac{1}{4}H{B^2} = \frac{1}{4}\left( {H{A^2} + H{B^2}} \right) = \frac{1}{4}A{B^2} = {R^2}\].
Vậy \[J{K^2} + J{G^2}\] có giá trị không đổi khi \[M\] di chuyển trên đường thẳng \[{d_1}\].
Lời giải
![]()
Điều kiện xác định: ![]() .
.
Ta có: ![]()
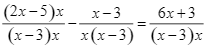
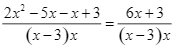
![]()
![]()
![]()
![]()
Suy ra ![]() (loại) hoặc
(loại) hoặc ![]() (TM).
(TM).
Vậy ![]() là nghiệm của phương trình.
là nghiệm của phương trình.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.