B. TRẮC NGHIỆM ĐÚNG - SAI. Thí sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Một hộp đựng 20 tấm thẻ cùng loại được đánh số từ 1 đến 20. Rút ngẫu nhiên một tấm thẻ trong hộp. Gọi \(A\) là biến cố “Rút được tấm thẻ ghi số chẵn lớn hơn 9”; \(B\) là biến cố “Rút được tấm thẻ ghi số từ 9 đến 14”.
a) \(A\) và \(B\) là hai biến cố xung khắc.
b) \(P\left( A \right) = \frac{3}{{10}}\).
c) \(P\left( {AB} \right) = \frac{1}{5}\).
d) \(P\left( {A \cup B} \right) = \frac{9}{{20}}\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
a) S, b) Đ, c) S, d) Đ
a) Ta có \(A = \left\{ {10;12;14;16;18;20} \right\}\); \(B = \left\{ {9;10;11;12;13;14} \right\}\).
Do \(A \cap B \ne \emptyset \) nên \(A\) và \(B\) không xung khắc.
b) Có \(P\left( A \right) = \frac{6}{{20}} = \frac{3}{{10}}\).
c) Ta có \(AB = \left\{ {10;12;14} \right\}\). Suy ra \(P\left( {AB} \right) = \frac{3}{{20}}\).
d) Có \(P\left( B \right) = \frac{6}{{20}} = \frac{3}{{10}}\).
\(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) = \frac{3}{{10}} + \frac{3}{{10}} - \frac{3}{{20}} = \frac{9}{{20}}\).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Trả lời: 60,5
Khối lượng Poloni còn lại sau 100 ngày là \(m\left( {100} \right) = 100.{\left( {\frac{1}{2}} \right)^{\frac{{100}}{{138}}}} \approx 60,5\) (gam).
Lời giải
Hướng dẫn giải
Trả lời: 60
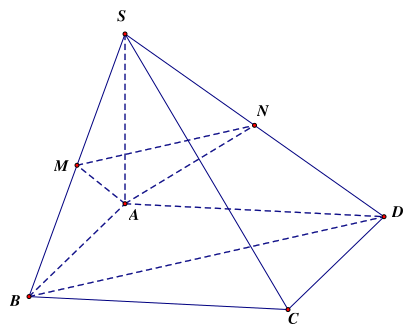
Gọi \(N\) là trung điểm của \(SD\).
Mà \(M\) là trung điểm của \(SB\)nên \(MN//BD\).
Do đó \(\left( {AM,BD} \right) = \left( {AM,MN} \right) = \widehat {AMN}\).
Ta có \(\Delta SAB\) vuông cân tại \(A\) nên \(SB = \sqrt {S{A^2} + A{B^2}} = a\sqrt 2 \).
mà \(AM\) là trung tuyến nên \(AM = \frac{{SB}}{2} = \frac{{a\sqrt 2 }}{2}\) (1).
Tương tự \(AN = \frac{{a\sqrt 2 }}{2}\) (2).
\(MN\) là đường trung bình của \(\Delta SBD\) nên \(MN = \frac{{BD}}{2} = \frac{{a\sqrt 2 }}{2}\) (3).
Từ (1), (2), (3) ta có \(\Delta AMN\) đều nên \(\left( {AM,BD} \right) = \widehat {AMN} = 60^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo