Cho đường tròn tâm O bán kính 6 cm và một điểm A cách O là 10 cm. Kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm). Tính độ dài AB.
A. AB = 12 cm.
B. AB = 4 cm.
C. AB = 6 cm.
D. AB = 8 cm.
Quảng cáo
Trả lời:
Đáp án đúng là: D
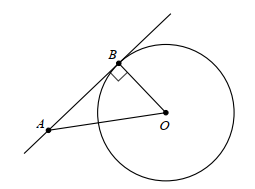
Vì AB là tiếp tuyến và B là tiếp điểm nên OB = R = 6 cm; AB ⊥ OB tại B.
Áp dụng định lí Pythagore vào tam giác ABO vuông tại B, ta được:
AB = \(\sqrt {O{A^2} - O{B^2}} = \sqrt {{{10}^2} - {6^2}} = 8\) cm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. AB = 8 cm.
B. AB = 12 cm.
C. AB = 23 cm.
D. AB = 6 cm.
Lời giải
Đáp án đúng là: B

Vì AB là tiếp tuyến và B là tiếp điểm nên OB = R = 5 cm; AB ⊥ OB tại B.
Áp dụng định lí Pythagore vào tam giác ABO vuông tại B, ta được:
AB = \(\sqrt {O{A^2} - O{B^2}} = \sqrt {{{13}^2} - {5^2}} = 12\) cm.
Câu 2
A. \(MK = R\sqrt 3 \).
B. MK = 2R.
C. MK = R.
D. \(MK = R\sqrt 2 \).
Lời giải
Đáp án đúng là: C
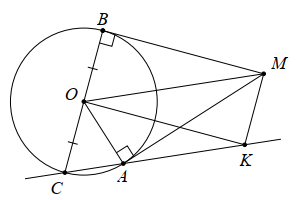
Xét đường tròn (O; R) có MA, MB là tiếp tuyến.
Suy ra \(\widehat {BOM} = \widehat {AOM} = \frac{1}{2}\widehat {AOB}\) (tính chất hai tiếp tuyến cắt nhau) (1).
∆OAC có OA = OC suy ra \(\widehat {OAC} = \widehat {OCA}\) (tính chất tam giác cân)
Ta có: \(\widehat {OAC} + \widehat {OCA} = \widehat {AOB}\) (tính chất góc ngoài của tam giác)
Từ (1) và (2) suy ra \(\widehat {OCA} = \widehat {BOM}\).
Mà \(\widehat {OCA},\widehat {BOM}\) ở vị trí đồng vị.
Nên CK ∕∕ OM suy ra \(\widehat {MOK} = \widehat {CKO}\) (so le trong).
Chứng minh ∆OAM = ∆OCK (c.g.c) suy ra CK = OM (hai cạnh tương ứng).
Chứng minh ∆KMO = ∆OCK (c.g.c) suy ra \(\widehat {COK} = \widehat {OKM}\) (hai góc .
tương ứng).
Mà \(\widehat {COK}\) = 90° (KO là trung trực của BC) suy ra \(\widehat {OKM}\) = 90°.
Xét tứ giác OBMK có:
\(\widehat {OBM}\) = 90° (MB là tiếp tuyến của (O; R)).
\(\widehat {BOK}\) = 90° (KO là trung trực của BC).
\(\widehat {OKM}\) = 90° (cmt)
Do đó OBMK là hình chữ nhật suy ra MK = OB = R.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(4\sqrt 3 \) cm.
B. 4 cm.
C. 12 cm.
D. \(2\sqrt 3 \) cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\frac{{120}}{{17}}\) cm.
B. 20 cm.
C. 17 cm.
D. \(\frac{{120}}{7}\) cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.