Câu hỏi:
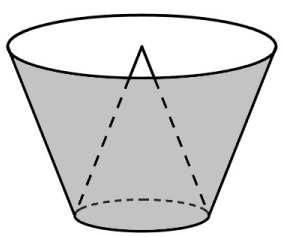
12/03/2025 143(0,5 điểm) Một cái thùng đựng nước được tạo thành từ việc cắt mặt xung quanh của một hình nón bởi một mặt phẳng vuông góc với trục của hình nón. Miệng thùng là đường tròn có bán kính bằng hai lần bán kính mặt đáy của thùng. Bên trong thùng có một cái phễu dạng hình nón có đáy là đáy của thùng, có đỉnh là tâm của miệng thùng (xem hình minh họa). Biết rằng đổ 12 lít nước vào thùng thì đầy thùng (nước không chảy được vào bên trong phễu), tính thể tích của phễu.
Quảng cáo
Trả lời:
Giải bởi Vietjack
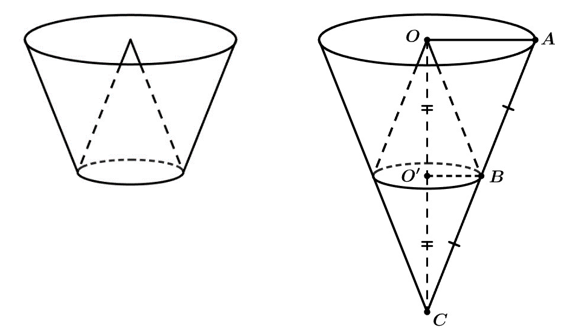
Đường sinh \[AB\] cắt trục \[OO'\] tại \[C.\] Khi đó hai hình nón có đỉnh \[O,\,\,C\] có chung đáy là hình tròn \[\left( {O'} \right)\] có thể tích bằng nhau.
Gọi \[{V_1}\] là thể tích hình nón đỉnh \[C,\] đáy là hình tròn \[\left( {O'} \right)\]; \[{V_2}\] là thể tích hình nón đỉnh \[O,\] đáy là hình tròn \[\left( {O'} \right)\]; \[V\] là thể tích hình nón đỉnh \[C,\] đáy là hình tròn \[\left( O \right)\];
\({V_n} = 12\) là thể tích nước đổ vào.
Ta có \[\frac{{{V_1}}}{V} = \frac{{\frac{1}{3} \cdot CO' \cdot \pi \cdot O'{B^2}}}{{\frac{1}{3} \cdot CO \cdot \pi \cdot O{A^2}}} = \frac{{CO'}}{{CO}} \cdot {\left( {\frac{{O'B}}{{OA}}} \right)^2} = \frac{1}{{\rm{2}}} \cdot {\left( {\frac{1}{2}} \right)^2} = \frac{1}{8}\].
Suy ra \[{V_1}\, = {V_2} = \frac{1}{8}V & \left( 1 \right)\].
Do đó thể tích nước đổ vào \({V_n} = \frac{6}{8}V\, & \left( 2 \right)\) (vì \[{V_1} + {V_2}\, + {V_n} = V\]).
Từ \[\left( 1 \right)\] và \(\left( 2 \right)\) suy ra \[{V_1} = {V_2} = \frac{1}{6}{V_n} = \frac{1}{6} \cdot 12 = 2\] l(ít).
Vậy thể tích của phễu là 2 lít.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
1) Bảng A của một giải Bóng đá gồm 4 đội bóng tham gia thi đấu, hai đội bóng bất kì thi đấu với nhau đúng một trận. Mỗi trận đấu, đội thua được 0 điểm, đội thắng được 3 điểm, hai đội hòa nhau mỗi đội được 1 điểm; số điểm của mỗi trận đấu bằng tổng số điểm của hai đội bóng tham gia trận đấu đó. Biết rằng tổng số điểm của tất cả các trận đấu bằng 16 điểm. Tính số trận hòa và số trận thắng (trận đấu có đội thắng, đội thua) của Bảng A.
Xem đáp án »
12/03/2025
344
Câu 3:
Gieo một con xúc xắc 50 lần cho kết quả như sau:
Số chấm xuất hiện
1
2
3
4
5
6
Tần số
8
7
?
8
6
11
Tần số xuất hiện mặt 3 chấm là
Gieo một con xúc xắc 50 lần cho kết quả như sau:
|
Số chấm xuất hiện |
1 |
2 |
3 |
4 |
5 |
6 |
|
Tần số |
8 |
7 |
? |
8 |
6 |
11 |
Xem đáp án »
12/03/2025
244
Câu 4:
1) Rút gọn biểu thức \(A = \sqrt {{{\left( { - 3} \right)}^2} \cdot 2} \,\, - \,\,\frac{{\sqrt 6 }}{{\sqrt 3 }}\) .
Xem đáp án »
12/03/2025
192
Câu 5:
1) Gọi \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình \(2{x^2} - 3x - 4 = 0\). Không giải phương trình, hãy tính giá trị của biểu thức \(A = {\left( {{x_1} + {x_2}} \right)^2} + {x_1}{x_2}\).
Xem đáp án »
12/03/2025
141
Câu 6:
Cho tam giác \[ABC\] vuông tại \[A.\] Khẳng định nào sau đây đúng?
Xem đáp án »
12/03/2025
98
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 9 Chân trời sáng tạo có đáp án (Đề số 1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận