Quảng cáo
Trả lời:
Vì \(MA,\,\,MD\) là các tiếp tuyến của \(\left( {{O_1}} \right)\) nên \(M{O_1}\) là phân giác của \(\widehat {AMD}.\)
Suy ra \(\widehat {AM{O_1}} = \frac{1}{2}\widehat {AMB} = \frac{1}{2}60^\circ = 30^\circ .\)
Do \(MA\) là tiếp tuyến của \(\left( {{O_1}} \right)\) nên \(MA \bot {O_1}A.\)
Xét \(\Delta MA{O_1}\) vuông tại \(A,\) ta có: \(\widehat {AM{O_1}} + \widehat {A{O_1}M} = 90^\circ \) (tổng hai góc nhọn của tam giác vuông).
Suy ra \(\widehat {A{O_1}M} = 90^\circ - \widehat {AM{O_1}} = 90^\circ - 30^\circ = 60^\circ .\)
Vì \(MA,\,\,MD\) là các tiếp tuyến của \(\left( {{O_1}} \right)\) nên \({O_1}M\) là phân giác của \(\widehat {A{O_1}D}.\)
Suy ra \(\widehat {A{O_1}D} = 2\widehat {A{O_1}M} = 2 \cdot 60^\circ = 120^\circ .\)
Do đó số đo cung nhỏ là
Như vậy, số đo cung lớn của đường tròn \(\left( {{O_1}} \right)\) là
Ta có số đo cung lớn của đường tròn \(\left( {{O_1}} \right)\) là \(240^\circ \) nên độ dài cung lớn của đường tròn \(\left( {{O_1}} \right)\) là: \({l_1} = \frac{{\pi \cdot 40 \cdot 240}}{{180}} = \frac{{160\pi }}{3}{\rm{\;(cm)}}{\rm{.}}\)
Câu hỏi cùng đoạn
Câu 2:
2) Tính độ dài dây cuaroa.
Tương tự câu 1, trong đường tròn \(\left( {{O_2}} \right)\) ta có: nên độ dài cung nhỏ của đường tròn \(\left( {{O_2}} \right)\) là: \({l_2} = \frac{{\pi \cdot 10 \cdot 120}}{{180}} = \frac{{20\pi }}{3}{\rm{\;(cm)}}{\rm{.}}\)
Xét \(\Delta M{O_1}A\) và \(\Delta M{O_2}B\) có: \(\widehat {MA{O_1}} = \widehat {MB{O_2}} = 90^\circ \) và \(\widehat {AM{O_1}}\) là góc chung
Do đó (g.g). Suy ra \(\frac{{MA}}{{MB}} = \frac{{{O_1}A}}{{{O_2}B}} = \frac{{40}}{{10}} = 4.\)
Nên \(MA = 4MB,\) suy ra \(AB = 3MB.\)
Xét \(\Delta M{O_2}B\) vuông tại\(B,\) ta có:
\(MB = {O_2}B \cdot \cot \widehat {BM{O_2}} = {O_2}B \cdot \cot 30^\circ = 10 \cdot \tan 60^\circ = 10\sqrt 3 {\rm{\;(cm)}}{\rm{.}}\)
Do đó \(AB = 3MB = 3 \cdot 10\sqrt 3 = 30\sqrt 3 {\rm{\;(cm)}}{\rm{.}}\)
Vậy độ dài của dây cua-roa là
\(2AB + {l_1} + {l_2} = 2 \cdot 30\sqrt 3 + \frac{{160\pi }}{3} + \frac{{20\pi }}{3} = 60\left( {\pi + \sqrt 3 } \right){\rm{\;(cm)}}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
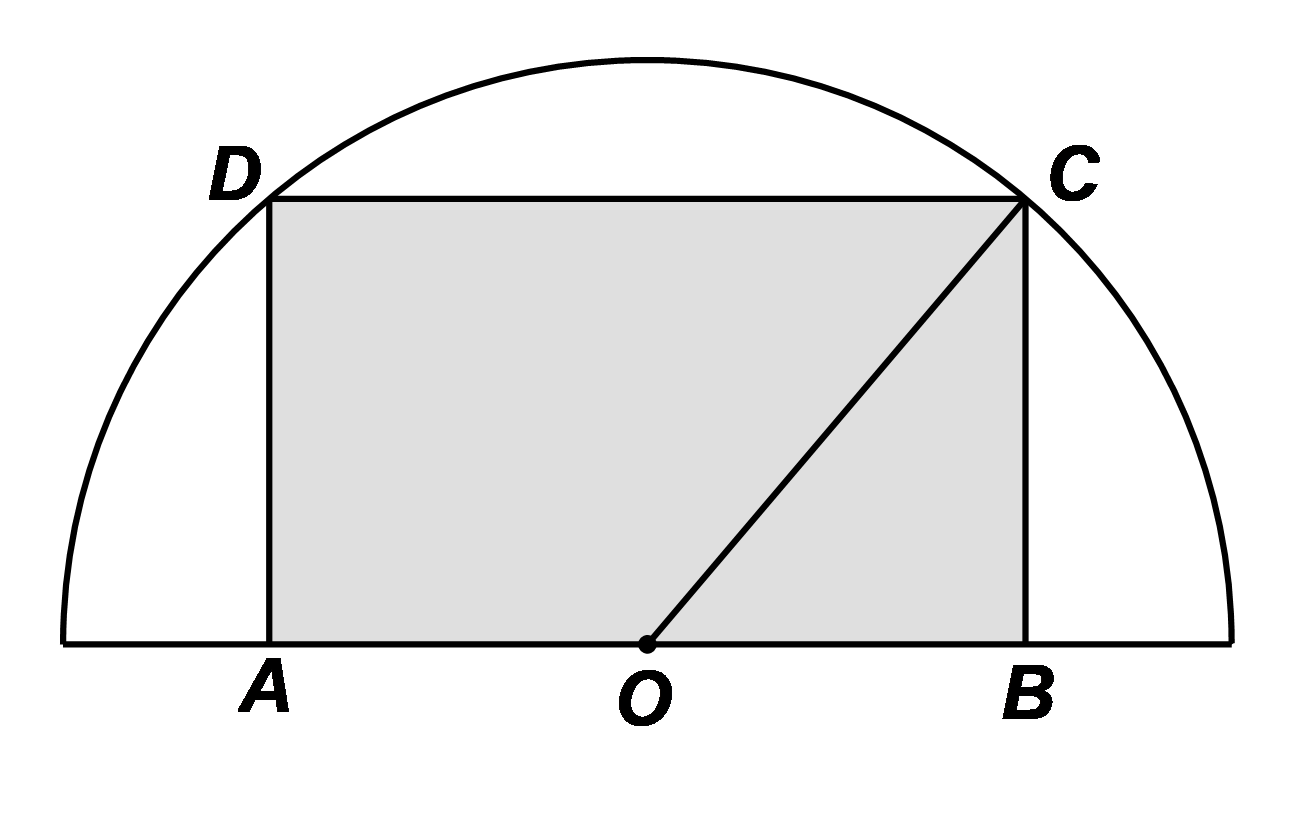
Gọi \(O\) là tâm hình bán nguyệt, đặt \(x = OB\) với \(x > 0.\)
Xét \(\Delta OBC\) vuông tại \(B,\) theo định lý Pythagore, ta có:
\(O{C^2} = O{B^2} + B{C^2},\) suy ra \(BC = \sqrt {O{C^2} - O{B^2}} = \sqrt {{R^2} - {x^2}} .\)Diện tích hình chữ nhật \(ABCD\) là:
\(S = AB \cdot BC = 2x \cdot \sqrt {{R^2} - {x^2}} = 2\sqrt {{x^2}\left( {{R^2} - {x^2}} \right)} \) \( \le {x^2} + \left( {{R^2} - {x^2}} \right) = {R^2}\) (Bất đẳng thức Cauchy).
Dấu “=” xảy ra khi và chỉ khi \({x^2} = {R^2} - {x^2}\) hay \[x = \frac{{R\sqrt 2 }}{2} = \frac{{20 \cdot \sqrt 2 }}{2} = 10\sqrt 2 {\rm{\;(cm)}}{\rm{.}}\]
Vậy diện tích hình chữ nhật lớn nhất bằng \({R^2}\) khi \(AB = 2 \cdot 10\sqrt 2 = 20\sqrt 2 \) (cm).
Lời giải
Giải bất phương trình:
\(x - 2 > 3\)
\[x > 3 + 2\]
\[x > 5.\]
Vậy bất phương trình có nghiệm là \[x > 5.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.