Câu 11-13:( 1 điểm)
2) Cho nửa đường tròn tâm \(O\) đường kính \(AB = 2R.\) Từ \(A\) và \(B\) lần lượt kẻ hai tiếp tuyến \(Ax\) và \(By\) với nửa đường tròn. Qua điểm \(M\) thuộc nửa đường tròn \((M\) khác \(A\) và \(B)\) kẻ tiếp tuyến thứ ba cắt các tiếp tuyến \(Ax\) và \(By\) lần lượt tại \(C\) và \(D\).
1) Biết rằng cả 3 thí sinh trong Câu lạc bộ Toán học đều có điểm thi không dưới 8. Chọn ngẫu nhiên 1 thí sinh của trường có điểm thi lớn hơn hoặc bằng 8. Tính xác suất để không có thí sinh của Câu lạc bộ Toán học nào được chọn.
Câu 11-13:( 1 điểm)
2) Cho nửa đường tròn tâm \(O\) đường kính \(AB = 2R.\) Từ \(A\) và \(B\) lần lượt kẻ hai tiếp tuyến \(Ax\) và \(By\) với nửa đường tròn. Qua điểm \(M\) thuộc nửa đường tròn \((M\) khác \(A\) và \(B)\) kẻ tiếp tuyến thứ ba cắt các tiếp tuyến \(Ax\) và \(By\) lần lượt tại \(C\) và \(D\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
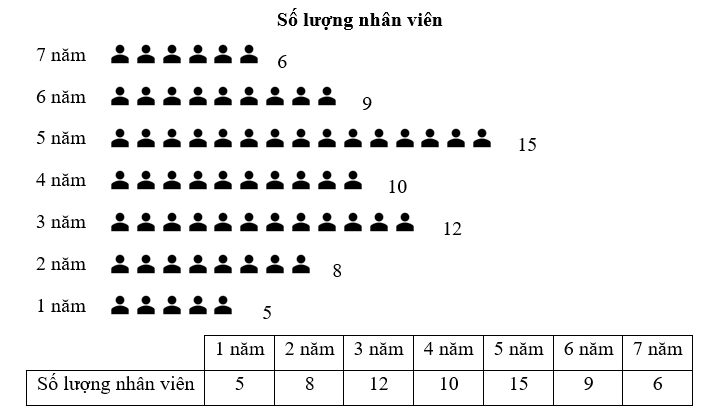
Ta có số thí sinh có điểm thi lớn hơn hoặc bằng 8 là \(11 + 5 = 16.\)
Chọn 1 thí sinh trong 16 thí sinh, không gian mẫu có 16 phần tử.
Gọi \[A\] là biến cố “Thí sinh của Câu lạc bộ Toán học không được chọn”.
Số thí sinh không thuộc Câu lạc bộ Toán học có điểm thi lớn hơn hoặc bằng 8 là \(16 - 3 = 13.\)
Chọn 1 thí sinh trong 13 thí sinh này. Có 13 kết quả thuận lợi cho biến cố \[A.\]
Vậy \(P\left( A \right) = \frac{{13}}{{16}}.\)
Câu hỏi cùng đoạn
Câu 2:
2) Biết 3 thí sinh trong Câu lạc bộ Toán học gồm có 1 thí sinh nam và 2 thí sinh nữ. Trong buổi lễ tuyên dương khen thưởng 3 thí sinh của Câu lạc bộ Toán học, 3 thí sinh được sắp xếp ngẫu nhiên thành một hàng ngang để trao quà. Tính xác suất để 2 thí sinh nữ không đứng cạnh nhau.
Giải bởi Vietjack
Kí hiệu 2 thí \(\sinh \) nữ là \({G_1}\) và \({G_2},\) thí \(\sinh \) nam là \[B.\]
Ta có không gian mẫu là: \[\Omega = \left\{ {{G_1}{G_2}B;\,\,{G_1}B{G_2};\,\,{G_2}{G_1}B;\,\,{G_2}B{G_1};\,\,B{G_1}{G_2};\,\,B{G_2}{G_1}} \right\}.\]
Không gian mẫu có 6 phần tử.
Gọi \[B\] là biến cố “Hai học nữ không đứng cạnh nhau”.
Ta có \(B = \left\{ {{G_1}B{G_2};\,\,{G_2}B{G_1}} \right\},\) có 2 kết quả thuận lợi cho biến cố \[B.\]
Vậy \(P\left( B \right) = \frac{2}{6} = \frac{1}{3}.\)
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
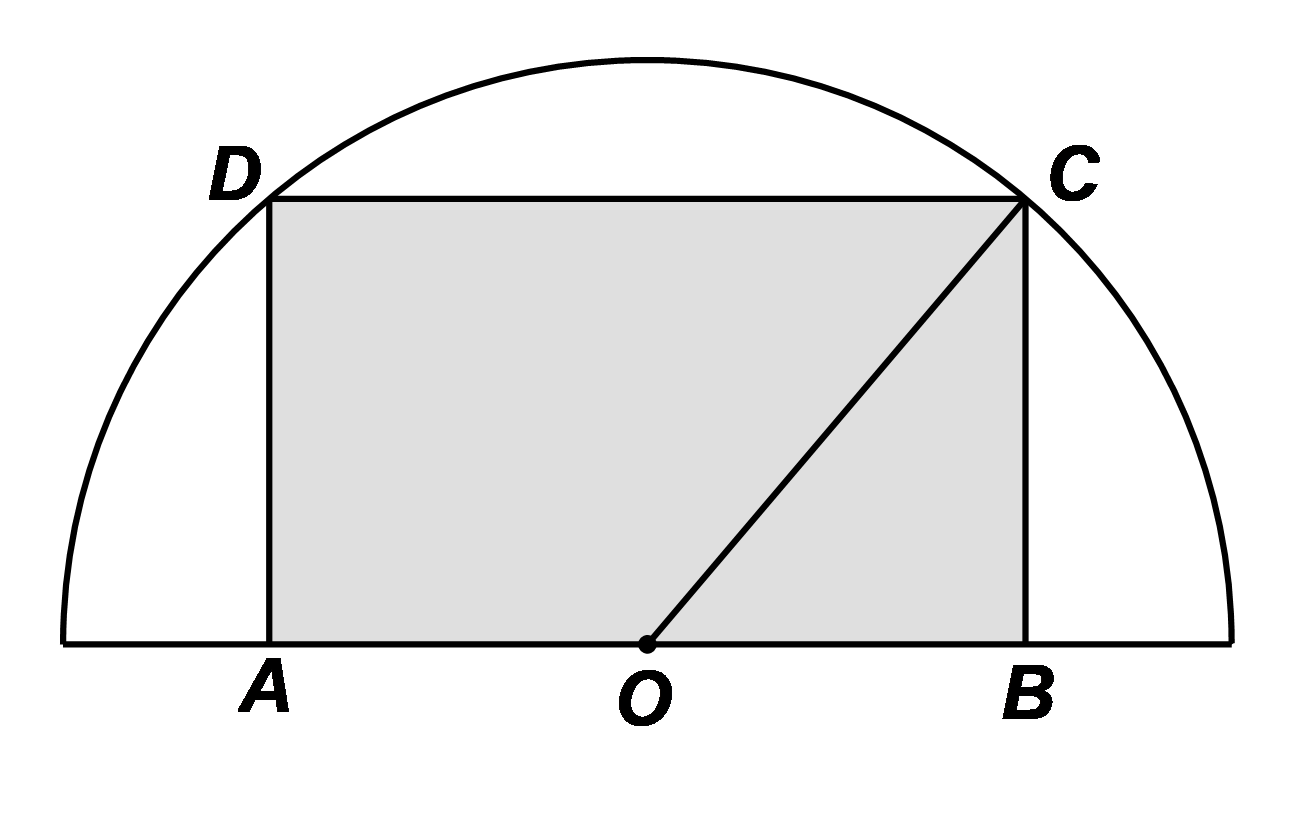
Gọi \(O\) là tâm hình bán nguyệt, đặt \(x = OB\) với \(x > 0.\)
Xét \(\Delta OBC\) vuông tại \(B,\) theo định lý Pythagore, ta có:
\(O{C^2} = O{B^2} + B{C^2},\) suy ra \(BC = \sqrt {O{C^2} - O{B^2}} = \sqrt {{R^2} - {x^2}} .\)Diện tích hình chữ nhật \(ABCD\) là:
\(S = AB \cdot BC = 2x \cdot \sqrt {{R^2} - {x^2}} = 2\sqrt {{x^2}\left( {{R^2} - {x^2}} \right)} \) \( \le {x^2} + \left( {{R^2} - {x^2}} \right) = {R^2}\) (Bất đẳng thức Cauchy).
Dấu “=” xảy ra khi và chỉ khi \({x^2} = {R^2} - {x^2}\) hay \[x = \frac{{R\sqrt 2 }}{2} = \frac{{20 \cdot \sqrt 2 }}{2} = 10\sqrt 2 {\rm{\;(cm)}}{\rm{.}}\]
Vậy diện tích hình chữ nhật lớn nhất bằng \({R^2}\) khi \(AB = 2 \cdot 10\sqrt 2 = 20\sqrt 2 \) (cm).
Lời giải
Giải bất phương trình:
\(x - 2 > 3\)
\[x > 3 + 2\]
\[x > 5.\]
Vậy bất phương trình có nghiệm là \[x > 5.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo