Câu hỏi:
06/05/2025 113
Câu 13-14. (1,5 điểm)
1) Nhà bác học Galileo Galilei (1564 – 1642) là người đầu tiên phát hiện ra quãng đường chuyển động của vật rơi tự do tỉ lệ thuận với bình phương của thời gian chuyển động. Liên hệ giữa quãng đường chuyển động \(S\) (mét) và thời gian chuyển động \(t\) (giây) được cho bởi hàm số \(S = 4,9{t^2}.\) Trong một thí nghiệm Vật lí, người ta thả một vật nặng rơi tự do từ độ cao \[122,5\] m xuống đất (coi sức cản của không khí không đáng kể).
a) Hỏi sau thời gian bao nhiêu giây vật nặng rơi tự do sẽ chạm đất?
b) Sau thời gian 3 giây vật nặng rơi tự do còn cách mặt đất bao nhiêu mét?
Câu 13-14. (1,5 điểm)
1) Nhà bác học Galileo Galilei (1564 – 1642) là người đầu tiên phát hiện ra quãng đường chuyển động của vật rơi tự do tỉ lệ thuận với bình phương của thời gian chuyển động. Liên hệ giữa quãng đường chuyển động \(S\) (mét) và thời gian chuyển động \(t\) (giây) được cho bởi hàm số \(S = 4,9{t^2}.\) Trong một thí nghiệm Vật lí, người ta thả một vật nặng rơi tự do từ độ cao \[122,5\] m xuống đất (coi sức cản của không khí không đáng kể).
a) Hỏi sau thời gian bao nhiêu giây vật nặng rơi tự do sẽ chạm đất?
b) Sau thời gian 3 giây vật nặng rơi tự do còn cách mặt đất bao nhiêu mét?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
1) a) Với \[S = 122,5\] m, ta có:
\(122,5 = 4,9{t^2}\)
\({t^2} = 122,5:4,9\)
\({t^2} = 25\)
\[t = 5\] (do \[t > 0)\]
Vậy sau 5 giây vật rơi tự do chạm đất.
b) Với \(t = 3\) giây ta có \(S = 4,9 \cdot {3^2} = 44,1\) (m).
Vậy vật nặng còn cách mặt đất là: \(122,5 - 44,1 = 78,4\) (m).
Câu hỏi cùng đoạn
Câu 2:
2) Biết phương trình \({x^2} - 2x - 5 = 0\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}.\) Không giải phương trình, hãy tính giá trị của biểu thức \(M = \left| {x_1^2 - x_2^2} \right|.\)
2) Biết phương trình \({x^2} - 2x - 5 = 0\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}.\) Không giải phương trình, hãy tính giá trị của biểu thức \(M = \left| {x_1^2 - x_2^2} \right|.\)
Lời giải của GV VietJack
2) Xét phương trình \({x^2} - 2x - 5 = 0.\)
Phương trình có \(\Delta ' = {1^2} - 1 \cdot \left( { - 5} \right) = 6 > 0\) nên phương trình này có hai nghiệm phân biệt \({x_1},\,\,{x_2}.\)
Theo định lí Viète ta có \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 2}\\{{x_1} \cdot {x_2} = - 5}\end{array}} \right.\).
Ta có: \(M = \left| {\left( {{x_1} - {x_2}} \right)\left( {{x_1} + {x_2}} \right)} \right| = \left| {{x_1} - {x_2}} \right| \cdot \left| {{x_1} + {x_2}} \right|\)
\( = 2\left| {{x_1} - {x_2}} \right|\)\( = 2\sqrt {{{\left( {{x_1} - {x_2}} \right)}^2}} \)
\( = 2\sqrt {x_1^2 - 2{x_1}{x_2} + x_2^2} \)
\( = 2\sqrt {{{\left( {{x_1} + {x_2}} \right)}^2} - 4{x_1}{x_2}} \)
\( = 2\sqrt {{2^2} - 4 \cdot \left( { - 5} \right)} \)\( = 4\sqrt 6 .\)
Vậy \(M = 4\sqrt 6 .\)
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
Điều kiện xác định của biểu thức \(P = 2025\sqrt {2026 - x} \) là \(2026 - x \ge 0\) tức là \(x \le 2026.\)
Lời giải
Hướng dẫn giải
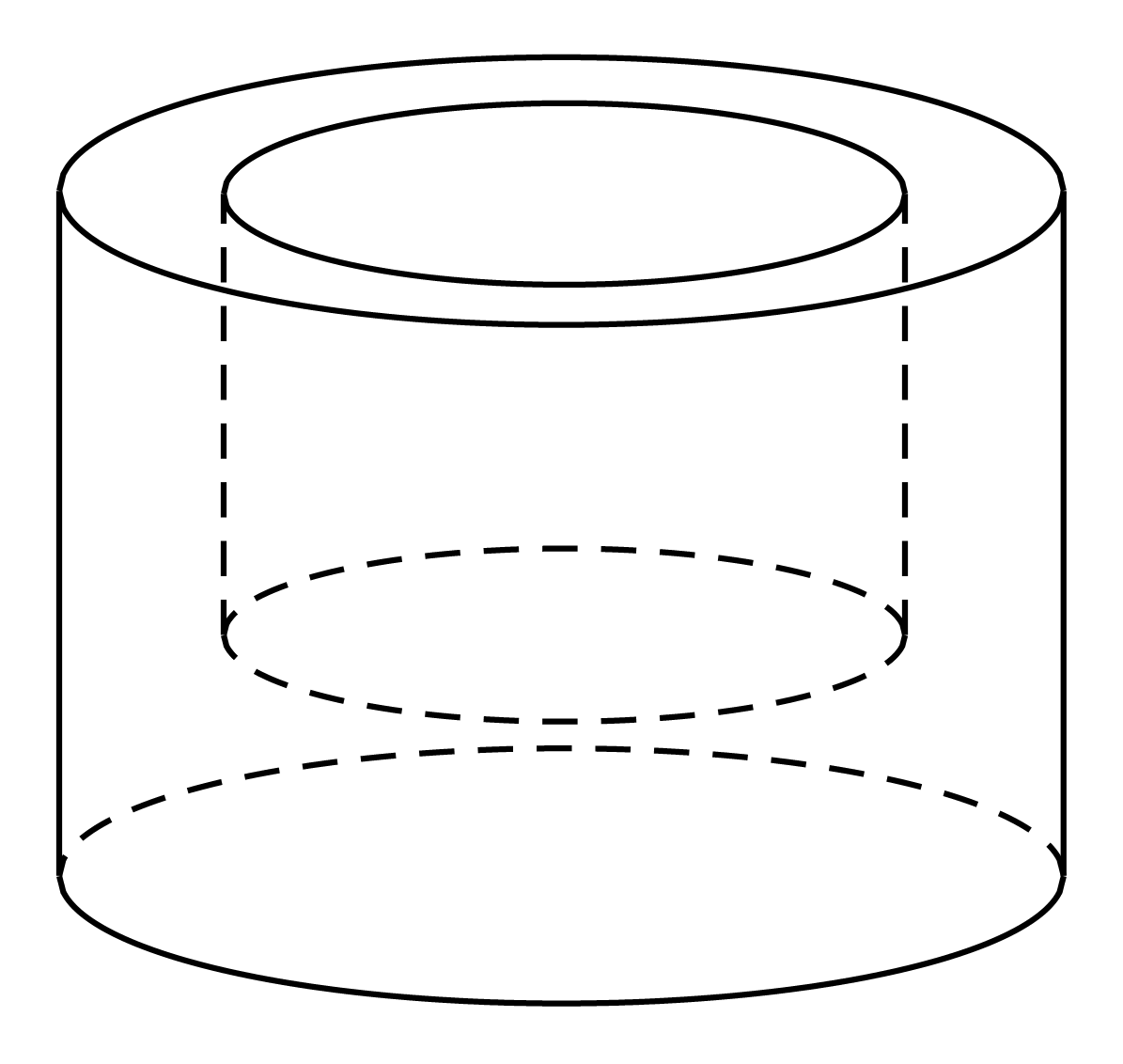
Thể tích chi tiết máy có dạng hình trụ với bán kính đáy bằng chiều cao và bằng 17 cm là:
\({V_1} = \pi r_1^2{h_1} = \pi \cdot {17^2} \cdot 17 = 4913\pi \)(cm2).
Thể tích lỗ khoan rồng có dạng hình trụ với bán kính đáy và độ sâu bằng 6 cm là:
\({V_2} = \pi r_2^2{h_2} = \pi \cdot {6^2} \cdot 6 = 216\pi \) (cm2).
Thể tích của phần chi tiết máy còn lại sau khi khoan là:
\[V = {V_1} - {V_2} = 4913\pi - 216\pi = 4697\pi = 14\,\,756,06\] (cm2).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo