Một nghiên cứu tại một trường đại học cho biết tỉ lệ sinh viên dùng cà phê để duy trì tỉnh táo khi học vào ban đêm là 70%. Giả sử chọn ngẫu nhiên 3 sinh viên từ nhóm khảo sát trên để phỏng vấn.
a) Xác suất để cả 3 sinh viên đều dùng cà phê để duy trì tỉnh táo là 0,343.
Một nghiên cứu tại một trường đại học cho biết tỉ lệ sinh viên dùng cà phê để duy trì tỉnh táo khi học vào ban đêm là 70%. Giả sử chọn ngẫu nhiên 3 sinh viên từ nhóm khảo sát trên để phỏng vấn.
a) Xác suất để cả 3 sinh viên đều dùng cà phê để duy trì tỉnh táo là 0,343.
Quảng cáo
Trả lời:
a) Đúng. Xác suất để cả 3 sinh viên đều dùng cà phê để duy trì tỉnh táo là \(0,{7^3} = 0,343\).
Câu hỏi cùng đoạn
Câu 2:
b) Xác suất trong 3 sinh viên có ít nhất 1 sinh viên không dùng cà phê là 0,657.
b) Xác suất trong 3 sinh viên có ít nhất 1 sinh viên không dùng cà phê là 0,657.
b) Đúng. Xác suất trong 3 sinh viên không có sinh viên nào không dùng cà phê là 0,343.
Nên xác suất trong 3 sinh viên có ít nhất 1 sinh viên không dùng cà phê là \[1 - 0,343 = 0,657.\]
Câu 3:
c) Xác suất trong 3 sinh viên có đúng 1 sinh viên dùng cà phê là 0,189.
c) Xác suất trong 3 sinh viên có đúng 1 sinh viên dùng cà phê là 0,189.
c) Đúng. Xác suất trong 3 sinh viên có đúng 1 sinh viên dùng cà phê là: \(0,7 \cdot 0,{3^2} \cdot C_3^1 = 0,189\).
Câu 4:
d) Xác suất trong 3 sinh viên có đúng 2 sinh viên dùng cà phê và 1 sinh viên không dùng cà phê lớn hơn 0,45.
d) Xác suất trong 3 sinh viên có đúng 2 sinh viên dùng cà phê và 1 sinh viên không dùng cà phê lớn hơn 0,45.
d) Sai. Xác suất trong 3 sinh viên có đúng 2 sinh viên dùng cà phê và 1 sinh viên không dùng cà phê là \(0,{7^2} \cdot 0,3 \cdot C_3^2 = 0,441\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 2189.
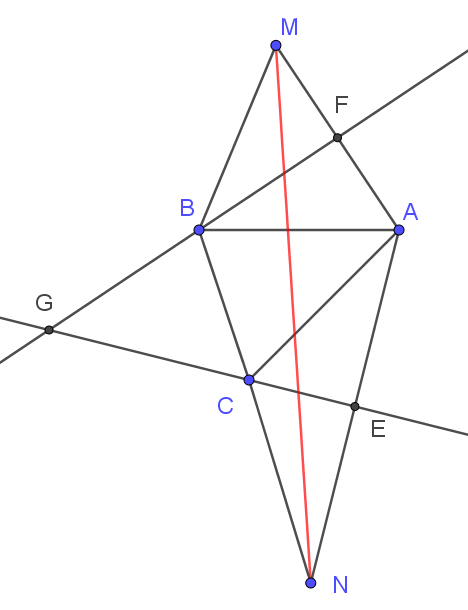
Do \({d_1} \cap {d_2} = G\left( { - 6;17;0} \right)\)\( \Rightarrow \left( {{d_1};{d_2}} \right) = \left( P \right):{\rm{ }}z = 0\).
+ \(M\)đối xứng với \(A\) qua \({d_1}\)
mp\(\left( Q \right)\) qua điểm \(A\) và vuông góc với \({d_1}\) có phương trình: \(x - 2y - 5 = 0\)
\(F = \left( Q \right) \cap {d_1} \Rightarrow F\left( {3; - 1;0} \right)\)
\(M\)đối xứng với \(A\) qua \({d_1}\)\( \Rightarrow F\)là trung điểm \(AM \Rightarrow M\left( {1; - 2;0} \right)\).
+ \(N\)đối xứng với \(A\) qua \({d_1}\)
mp\(\left( R \right)\) qua điểm \(A\) và vuông góc với \({d_2}\) có phương trình: \(x - y - 5 = 0\)
\(E = \left( R \right) \cap {d_2} \Rightarrow E\left( {8;3;0} \right)\)
\(N\)đối xứng với \(A\) qua \({d_2}\)\( \Rightarrow E\)là trung điểm \(AN \Rightarrow N\left( {11;6;0} \right)\)
+ Ta có \(P = AB + BC + CA = BM + BC + CN \ge MN\).
Suy ra \({P_{\min }} = MN = \sqrt {{{\left( {11 - 1} \right)}^2} + {{\left( {6 + 2} \right)}^2}} = \sqrt {164} \).
Vậy \(a + 2025 = 164 + 2025 = 2189\).
Lời giải
a) Đúng. Ta có lợi nhuận khi bán được \(50\) sản phẩm đầu tiên là:
\(\int\limits_0^{50} {P'\left( x \right){\rm{d}}x = } \int\limits_0^{50} {\left( { - 0,0008x + 10,4} \right){\rm{d}}x = 519} \) (triệu đồng).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.