Một căn bệnh có 1% dân số mắc phải. Một phương pháp chẩn đoán căn bệnh nói trên có tỉ lệ chính xác là 98% (với cả người bị bệnh và người không bị bệnh). Biết rằng nếu một người được sử dụng phương pháp trên để kiểm tra và cho kết quả dương tính (bị bệnh) thì xác suất người đó thực sự bị bệnh là \(\frac{y}{{148}},\) \(y\) là số tự nhiên. Hỏi \(y\) bằng bao nhiêu?
Một căn bệnh có 1% dân số mắc phải. Một phương pháp chẩn đoán căn bệnh nói trên có tỉ lệ chính xác là 98% (với cả người bị bệnh và người không bị bệnh). Biết rằng nếu một người được sử dụng phương pháp trên để kiểm tra và cho kết quả dương tính (bị bệnh) thì xác suất người đó thực sự bị bệnh là \(\frac{y}{{148}},\) \(y\) là số tự nhiên. Hỏi \(y\) bằng bao nhiêu?
Quảng cáo
Trả lời:
Đáp án: 49.
Gọi \(H\) là biến cố: “Người được sử dụng phương pháp chẩn đoán trên là người bị mắc bệnh”.
Hệ \(\left\{ {H;\,\,\bar H} \right\}\) là hệ đầy đủ biến cố với \(P\left( H \right) = 0,01\) và \(P\left( {\bar H} \right) = 0,99\).
Gọi \(A\) là biến cố: “Chẩn đoán cho kết quả dương tính”.
Ta có \(P\left( {A|H} \right) = 0,98;\,\,P\left( {A|\bar H} \right) = 0,02\).
Ta cần tìm xác suất \(P\left( {H|A} \right)\).
Áp dụng công thức xác suất Bayes, ta có
\(P\left( {H|A} \right) = \frac{{P\left( H \right) \cdot P\left( {A|H} \right)}}{{P\left( H \right) \cdot P\left( {A|H} \right) + P\left( {\bar H} \right) \cdot P\left( {A|\bar H} \right)}} = \frac{{0,01 \cdot 0,98}}{{0,01 \cdot 0,98 + 0,99 \cdot 0,02}} = \frac{{49}}{{148}}.\)
Vậy giá trị của \(y\) là \(49.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 2189.
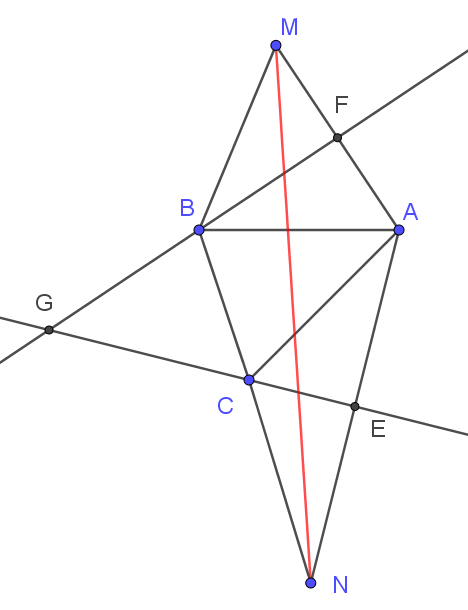
Do \({d_1} \cap {d_2} = G\left( { - 6;17;0} \right)\)\( \Rightarrow \left( {{d_1};{d_2}} \right) = \left( P \right):{\rm{ }}z = 0\).
+ \(M\)đối xứng với \(A\) qua \({d_1}\)
mp\(\left( Q \right)\) qua điểm \(A\) và vuông góc với \({d_1}\) có phương trình: \(x - 2y - 5 = 0\)
\(F = \left( Q \right) \cap {d_1} \Rightarrow F\left( {3; - 1;0} \right)\)
\(M\)đối xứng với \(A\) qua \({d_1}\)\( \Rightarrow F\)là trung điểm \(AM \Rightarrow M\left( {1; - 2;0} \right)\).
+ \(N\)đối xứng với \(A\) qua \({d_1}\)
mp\(\left( R \right)\) qua điểm \(A\) và vuông góc với \({d_2}\) có phương trình: \(x - y - 5 = 0\)
\(E = \left( R \right) \cap {d_2} \Rightarrow E\left( {8;3;0} \right)\)
\(N\)đối xứng với \(A\) qua \({d_2}\)\( \Rightarrow E\)là trung điểm \(AN \Rightarrow N\left( {11;6;0} \right)\)
+ Ta có \(P = AB + BC + CA = BM + BC + CN \ge MN\).
Suy ra \({P_{\min }} = MN = \sqrt {{{\left( {11 - 1} \right)}^2} + {{\left( {6 + 2} \right)}^2}} = \sqrt {164} \).
Vậy \(a + 2025 = 164 + 2025 = 2189\).
Lời giải
a) Đúng. Xác suất để cả 3 sinh viên đều dùng cà phê để duy trì tỉnh táo là \(0,{7^3} = 0,343\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.