PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Trong một phòng thí nghiệm có máy đo nồng độ khí \(C{O_2}\) cho thấy: nồng độ khí \(C{O_2}\) trong phòng thay đổi theo thời gian \(t\) (tính bằng giờ) và được thể hiện qua hàm số \(f\left( t \right) = 400 + \frac{{2000t}}{{{t^2} + 5}}\) \(\left( {{\rm{ppm}}} \right)\) với \(t \ge 0\) (khi nói nồng độ khí \(C{O_2}\) trong không khí là 400 ppm, điều đó có nghĩa là trong một triệu phần thể tích của không khí, có 400 phần thể tích là khí \(C{O_2}\)).
a) Nồng độ khí \(C{O_2}\) trong phòng tại thời điểm \(t = 0\) là 400 \(\left( {{\rm{ppm}}} \right)\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Trong một phòng thí nghiệm có máy đo nồng độ khí \(C{O_2}\) cho thấy: nồng độ khí \(C{O_2}\) trong phòng thay đổi theo thời gian \(t\) (tính bằng giờ) và được thể hiện qua hàm số \(f\left( t \right) = 400 + \frac{{2000t}}{{{t^2} + 5}}\) \(\left( {{\rm{ppm}}} \right)\) với \(t \ge 0\) (khi nói nồng độ khí \(C{O_2}\) trong không khí là 400 ppm, điều đó có nghĩa là trong một triệu phần thể tích của không khí, có 400 phần thể tích là khí \(C{O_2}\)).
a) Nồng độ khí \(C{O_2}\) trong phòng tại thời điểm \(t = 0\) là 400 \(\left( {{\rm{ppm}}} \right)\).
Quảng cáo
Trả lời:
a) Đúng. Nồng độ khí \(C{O_2}\) trong phòng tại thời điểm \(t = 0\) là
\(f\left( 0 \right) = 400 + \frac{{2000 \cdot 0}}{{{0^2} + 5}} = 400\) \(\left( {{\rm{ppm}}} \right)\).
Câu hỏi cùng đoạn
Câu 2:
b) \(f'\left( t \right) = \frac{{ - 2000{t^2} - 10000}}{{{{\left( {{t^2} + 5} \right)}^2}}}\) với \(t \ge 0\).
b) \(f'\left( t \right) = \frac{{ - 2000{t^2} - 10000}}{{{{\left( {{t^2} + 5} \right)}^2}}}\) với \(t \ge 0\).
b) Sai.
\[f'\left( t \right) = {\left( {400} \right)^\prime } + \frac{{{{\left( {2000t} \right)}^\prime }\left( {{t^2} + 5} \right) - {{\left( {{t^2} + 5} \right)}^\prime }2000t}}{{{{\left( {{t^2} + 5} \right)}^2}}} = \frac{{2000\left( {{t^2} + 5} \right) - 2t.2000t}}{{{{\left( {{t^2} + 5} \right)}^2}}}\]\[ = \frac{{ - 2000{t^2} + 10000}}{{{{\left( {{t^2} + 5} \right)}^2}}}\].
Câu 3:
c) Nghiệm của phương trình \[f'\left( t \right) = 0\] là \(t = 2\).
c) Nghiệm của phương trình \[f'\left( t \right) = 0\] là \(t = 2\).
c) Sai. \[f'\left( t \right) = 0 \Leftrightarrow \frac{{ - 2000{t^2} + 10000}}{{{{\left( {{t^2} + 5} \right)}^2}}} = 0 \Leftrightarrow - 2000{t^2} + 10000 = 0 \Leftrightarrow t = \sqrt 5 \] (vì \(t \ge 0\)).
Câu 4:
d) Nồng độ khí \(C{O_2}\) cao nhất đo được trong phòng thí nghiệm (làm tròn kết quả đến hàng đơn vị) là 947 \(\left( {{\rm{ppm}}} \right)\).
d) Nồng độ khí \(C{O_2}\) cao nhất đo được trong phòng thí nghiệm (làm tròn kết quả đến hàng đơn vị) là 947 \(\left( {{\rm{ppm}}} \right)\).
d) Sai. Ta có bảng biến thiên:
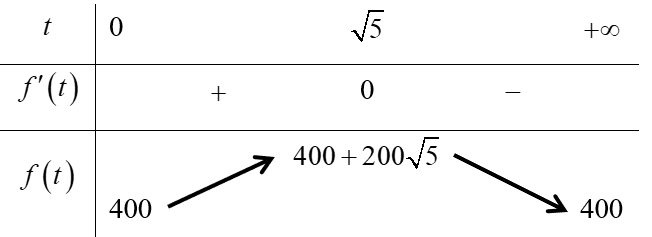
Vậy \[\mathop {\max }\limits_{\left[ {0; + \infty } \right)} f\left( t \right) = 400 + 200\sqrt 5 \approx 847\].
Do đó nồng độ khí \(C{O_2}\) cao nhất đo được trong phòng thí nghiệm (làm tròn kết quả đến hàng đơn vị) là 847 \(\left( {{\rm{ppm}}} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 0,36.
Gọi biến cố \(A\): “Ít nhất một trong hai người đó gọi đúng số điện thoại đã quên mà không phải thử quá hai lần”.
Khi đó, biến cố \(\bar A\): “Cả hai người gọi thử cả 2 lần đều không đúng”.
Xác suất gọi sai cả 2 lần của mỗi người là \(\frac{9}{{10}} \cdot \frac{8}{9} = \frac{4}{5}\).
Hai người gọi điện là độc lập nên \[P\left( {\overline A } \right) = \frac{4}{5} \cdot \frac{4}{5} = \frac{{16}}{{25}}\].
Vậy \(P\left( A \right) = 1 - \frac{{16}}{{25}} = \frac{9}{{25}} = 0,36\).
Lời giải
Đáp án: 12,4.
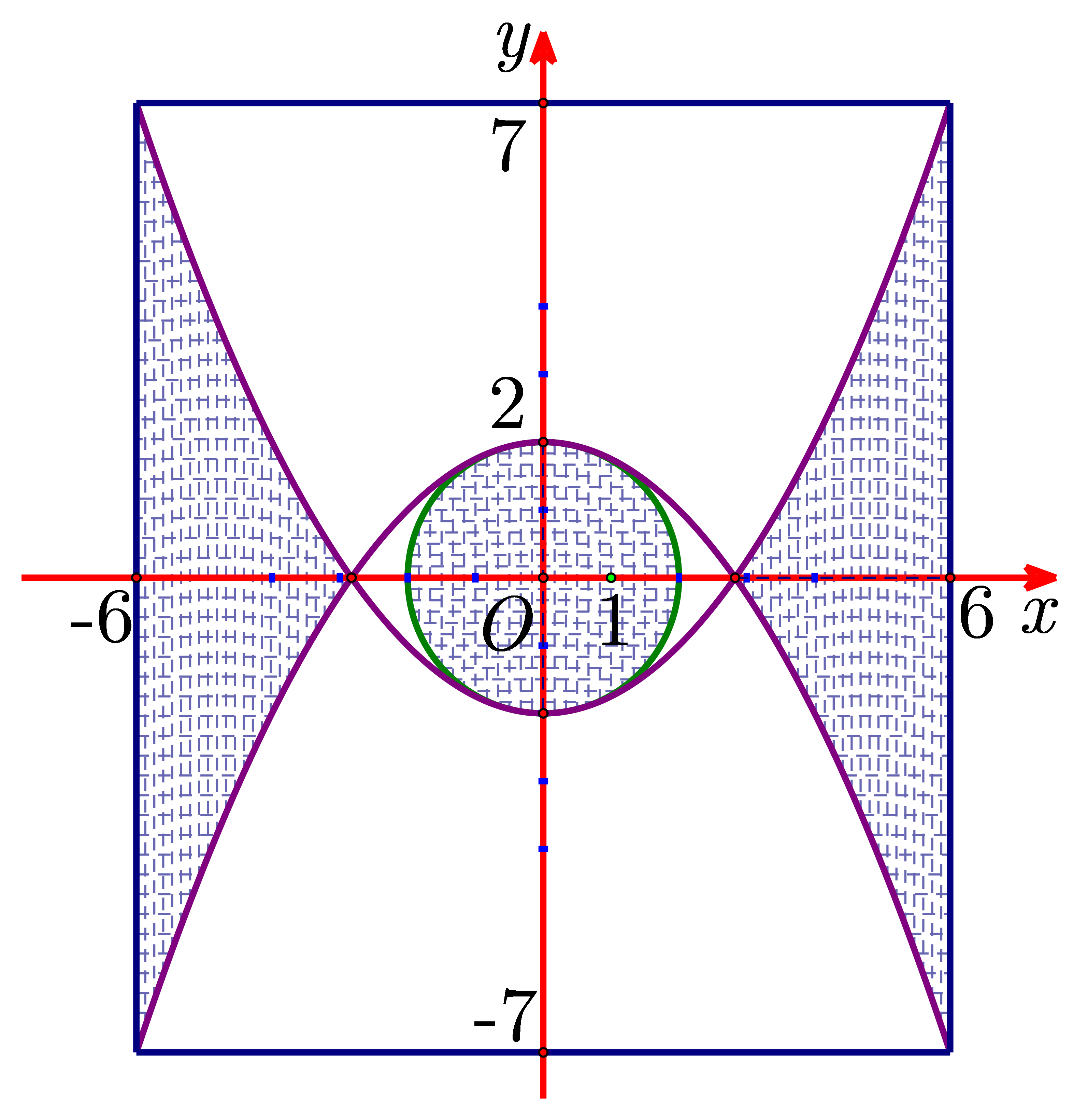
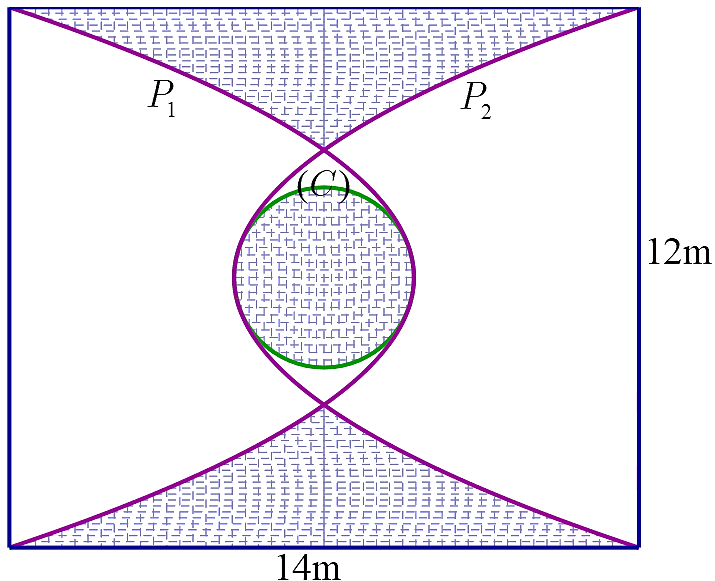
Chọn hệ trục tọa độ \(Oxy\) như hình vẽ với \(M\left( {0\,;\,m} \right)\,\,\left( {m < 0} \right)\) là đỉnh của parabol \(\left( {{P_1}} \right)\).
Khi đó \(\left( {{P_1}} \right):y = \frac{{7 - m}}{{36}}{x^2} + m\) và \(\left( C \right):{x^2} + {y^2} = {m^2}.\)
Để \(\left( {{P_1}} \right),\,\,\left( C \right)\) có một điểm chung duy nhất thì phương trình sau có nghiệm duy nhất.
\({x^2} + {\left( {\frac{{7 - m}}{{36}}{x^2} + m} \right)^2} = {m^2} \Leftrightarrow {x^2}\left[ {{{\left( {\frac{{7 - m}}{{36}}} \right)}^2}{x^2} + \frac{{ - {m^2} + 7m + 18}}{{18}}} \right] = 0\).
\({\rm{YCBT}} \Leftrightarrow - {m^2} + 7m + 18 \ge 0 \Leftrightarrow - 2 \le m \le 9\). Mà \(m < 0\) nên \( - 2 \le m < 0\).
Khi đó, đường tròn \(\left( C \right)\) có diện tích lớn nhất khi \(\left( C \right)\) có bán kính lớn nhất, điều này xảy ra khi và chỉ khi \(m = - 2 \Rightarrow r = 2.\)
Hoành độ giao điểm của \(\left( {{P_1}} \right):y = \frac{1}{4}{x^2} - 2\) và trục hoành là \(x = \pm 2\sqrt 2 \).
Diện tích phần lát gạch là \(S = 4\int\limits_{2\sqrt 2 }^6 {\left( {\frac{1}{4}{x^2} - 2} \right){\rm{d}}x} + \pi {r^2} = \frac{{72 + 32\sqrt 2 }}{3} + 4\pi \).
Số tiền lát gạch là: \(240S \approx 12396,32\) (nghìn đồng) \( \approx 12,4\) (triệu đồng).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.