Một công ty tổ chức chương trình bốc thăm trúng thưởng nhân dịp lễ 30/4 và 1/5 cho 100 nhân viên. Trong hộp có 100 vé, trong đó có 4 vé trúng thưởng tour du lịch miễn phí ở Thái Lan, 10 vé trúng thưởng tour du lịch miễn phí ở Đà Nẵng và 20 vé trúng thưởng tour du lịch miễn phí ở Cửa Lò (Nghệ An). Các vé còn lại trúng thưởng năm triệu đồng. Lần lượt từng nhân viên lên bốc ngẫu nhiên một vé (không hoàn lại).
a) Xác suất để người bốc thăm thứ nhất bốc được vé trúng thưởng năm triệu đồng là \[\frac{{33}}{{50}}\].
Một công ty tổ chức chương trình bốc thăm trúng thưởng nhân dịp lễ 30/4 và 1/5 cho 100 nhân viên. Trong hộp có 100 vé, trong đó có 4 vé trúng thưởng tour du lịch miễn phí ở Thái Lan, 10 vé trúng thưởng tour du lịch miễn phí ở Đà Nẵng và 20 vé trúng thưởng tour du lịch miễn phí ở Cửa Lò (Nghệ An). Các vé còn lại trúng thưởng năm triệu đồng. Lần lượt từng nhân viên lên bốc ngẫu nhiên một vé (không hoàn lại).
a) Xác suất để người bốc thăm thứ nhất bốc được vé trúng thưởng năm triệu đồng là \[\frac{{33}}{{50}}\].
Quảng cáo
Trả lời:
a) Đúng. Gọi \(A\) là biến cố: “Người bốc thăm thứ nhất bốc được vé trúng thưởng năm triệu đồng”. Khi đó hệ \(\left\{ {A\,;\,\overline A } \right\}\) là một hệ đầy đủ các biến cố.
Ta có \(n\left( A \right) = 100 - 4 - 10 - 20 = 66 \Rightarrow P\left( A \right) = \frac{{66}}{{100}} = \frac{{33}}{{50}}.\)
Câu hỏi cùng đoạn
Câu 2:
b) Xác suất để người bốc thăm thứ hai bốc được vé trúng thưởng năm triệu đồng là \[\frac{{13}}{{20}}\], biết rằng người bốc thăm thứ nhất bốc được vé trúng thưởng năm triệu đồng.
b) Xác suất để người bốc thăm thứ hai bốc được vé trúng thưởng năm triệu đồng là \[\frac{{13}}{{20}}\], biết rằng người bốc thăm thứ nhất bốc được vé trúng thưởng năm triệu đồng.
b) Sai. Gọi \(B\) là biến cố: “Người bốc thăm thứ hai bốc được vé trúng thưởng năm triệu đồng”.
Khi đó, xác suất để người bốc thăm thứ hai bốc được vé trúng thưởng năm triệu đồng, biết rằng người bốc thăm thứ nhất bốc được vé trúng thưởng năm triệu đồng là \(P\left( {B|A} \right) = \frac{{65}}{{99}}\).
Câu 3:
c) Xác suất để người bốc thăm thứ hai bốc được vé trúng thưởng năm triệu đồng là \[\frac{{33}}{{50}}\].
c) Xác suất để người bốc thăm thứ hai bốc được vé trúng thưởng năm triệu đồng là \[\frac{{33}}{{50}}\].
c) Đúng. Xác suất để người bốc thăm thứ hai bốc được vé trúng thưởng năm triệu đồng là \[P\left( B \right).\]
Áp dụng công thức xác suất toàn phần, ta có \[P\left( B \right) = P\left( A \right) \cdot P\left( {B|A} \right) + P\left( {\overline A } \right) \cdot P\left( {B|\overline A } \right)\].
Ta có \(P\left( {\overline A } \right) = 1 - \frac{{33}}{{50}} = \frac{{17}}{{50}}\), \[P\left( {B|\overline A } \right) = \frac{{66}}{{99}}\].
Vậy \[P\left( B \right) = P\left( A \right) \cdot P\left( {B|A} \right) + P\left( {\overline A } \right) \cdot P\left( {B|\overline A } \right) = \frac{{33}}{{50}} \cdot \frac{{65}}{{99}} + \frac{{17}}{{50}} \cdot \frac{{66}}{{99}} = \frac{{33}}{{50}}\].
Câu 4:
d) Để tạo bất ngờ cho người bốc thăm tiếp theo, sau khi người thứ nhất bốc thăm, người dẫn chương trình giữ lại vé và không công bố kết quả. Người bốc thăm thứ hai bốc được vé trúng thưởng năm triệu đồng. Xác suất để người bốc thăm thứ nhất bốc được vé trúng thưởng năm triệu đồng là \[\frac{{65}}{{99}}\].
d) Để tạo bất ngờ cho người bốc thăm tiếp theo, sau khi người thứ nhất bốc thăm, người dẫn chương trình giữ lại vé và không công bố kết quả. Người bốc thăm thứ hai bốc được vé trúng thưởng năm triệu đồng. Xác suất để người bốc thăm thứ nhất bốc được vé trúng thưởng năm triệu đồng là \[\frac{{65}}{{99}}\].
d) Đúng. Ta có \(P\left( {A|B} \right) = \frac{{P\left( {BA} \right)}}{{P\left( B \right)}} = \frac{{P\left( A \right) \cdot P\left( {B|A} \right)}}{{P\left( B \right)}} = \frac{{\frac{{33}}{{50}} \cdot \frac{{65}}{{99}}}}{{\frac{{33}}{{50}}}} = \frac{{65}}{{99}}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 0,36.
Gọi biến cố \(A\): “Ít nhất một trong hai người đó gọi đúng số điện thoại đã quên mà không phải thử quá hai lần”.
Khi đó, biến cố \(\bar A\): “Cả hai người gọi thử cả 2 lần đều không đúng”.
Xác suất gọi sai cả 2 lần của mỗi người là \(\frac{9}{{10}} \cdot \frac{8}{9} = \frac{4}{5}\).
Hai người gọi điện là độc lập nên \[P\left( {\overline A } \right) = \frac{4}{5} \cdot \frac{4}{5} = \frac{{16}}{{25}}\].
Vậy \(P\left( A \right) = 1 - \frac{{16}}{{25}} = \frac{9}{{25}} = 0,36\).
Lời giải
Đáp án: 12,4.
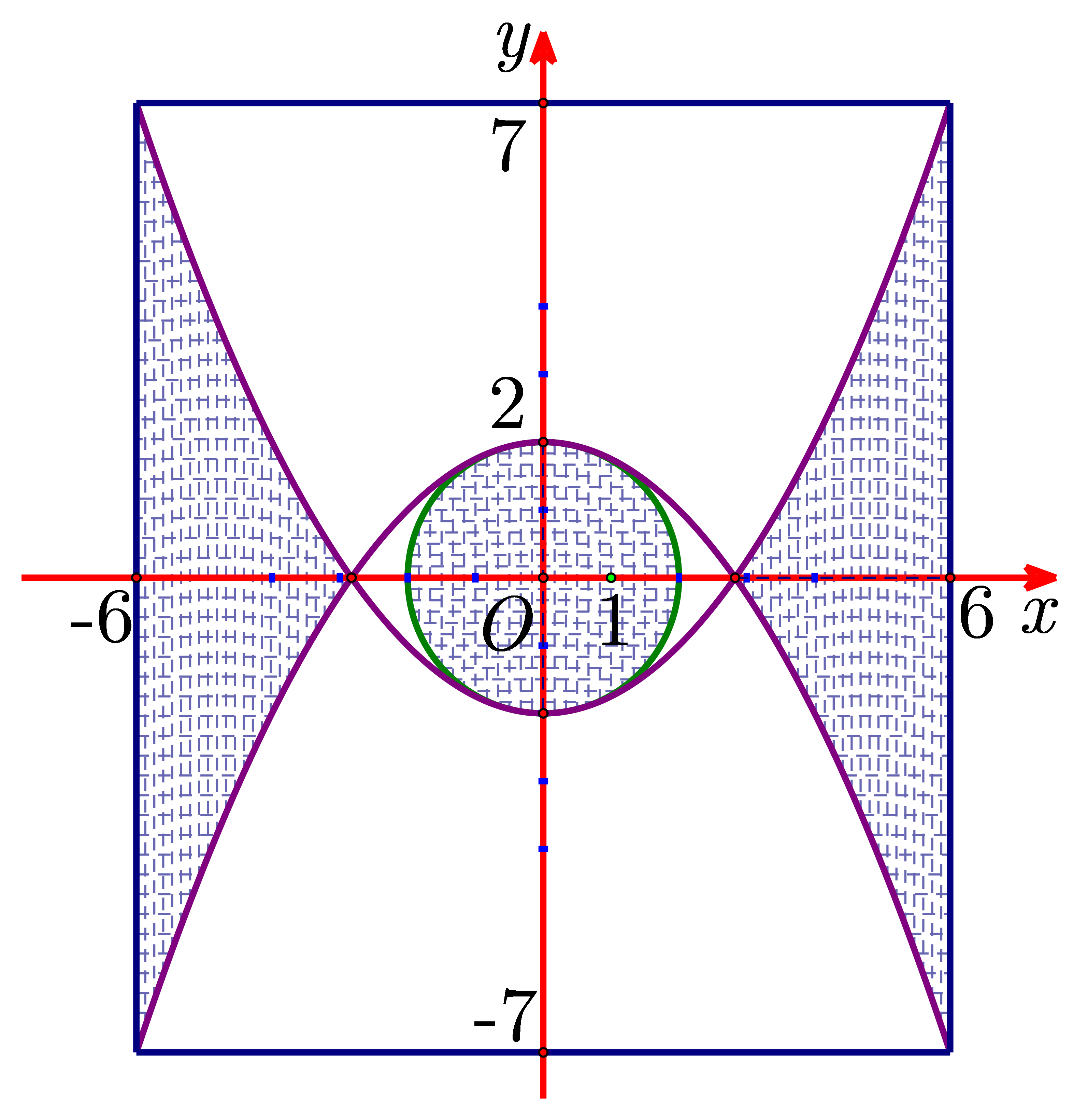
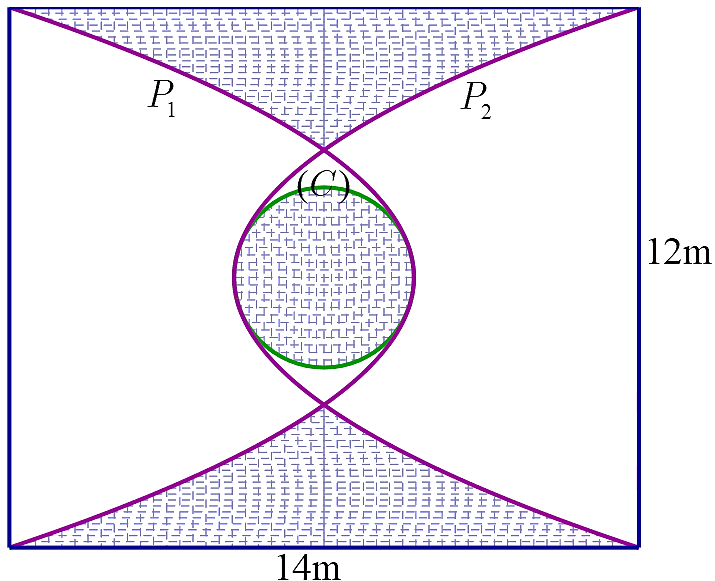
Chọn hệ trục tọa độ \(Oxy\) như hình vẽ với \(M\left( {0\,;\,m} \right)\,\,\left( {m < 0} \right)\) là đỉnh của parabol \(\left( {{P_1}} \right)\).
Khi đó \(\left( {{P_1}} \right):y = \frac{{7 - m}}{{36}}{x^2} + m\) và \(\left( C \right):{x^2} + {y^2} = {m^2}.\)
Để \(\left( {{P_1}} \right),\,\,\left( C \right)\) có một điểm chung duy nhất thì phương trình sau có nghiệm duy nhất.
\({x^2} + {\left( {\frac{{7 - m}}{{36}}{x^2} + m} \right)^2} = {m^2} \Leftrightarrow {x^2}\left[ {{{\left( {\frac{{7 - m}}{{36}}} \right)}^2}{x^2} + \frac{{ - {m^2} + 7m + 18}}{{18}}} \right] = 0\).
\({\rm{YCBT}} \Leftrightarrow - {m^2} + 7m + 18 \ge 0 \Leftrightarrow - 2 \le m \le 9\). Mà \(m < 0\) nên \( - 2 \le m < 0\).
Khi đó, đường tròn \(\left( C \right)\) có diện tích lớn nhất khi \(\left( C \right)\) có bán kính lớn nhất, điều này xảy ra khi và chỉ khi \(m = - 2 \Rightarrow r = 2.\)
Hoành độ giao điểm của \(\left( {{P_1}} \right):y = \frac{1}{4}{x^2} - 2\) và trục hoành là \(x = \pm 2\sqrt 2 \).
Diện tích phần lát gạch là \(S = 4\int\limits_{2\sqrt 2 }^6 {\left( {\frac{1}{4}{x^2} - 2} \right){\rm{d}}x} + \pi {r^2} = \frac{{72 + 32\sqrt 2 }}{3} + 4\pi \).
Số tiền lát gạch là: \(240S \approx 12396,32\) (nghìn đồng) \( \approx 12,4\) (triệu đồng).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.