Nhằm thu hút du khách và khẳng định vị thế dẫn đầu, công viên nước Đầm Sen quyết định đầu tư xây dựng một đường trượt nước độc đáo có mặt cắt được gắn vào hệ trục \(Oxy\) (xem trục \(Ox\) là mặt đất) với đơn vị mỗi trục là \(1\,{\rm{m}}\) như hình vẽ dưới đây. Đường trượt được thiết kế theo hình dạng của một hàm bậc ba \(y = g\left( x \right)\), với mục tiêu tối ưu hóa trải nghiệm của người dùng , một phần đường trượt được đặt dưới mặt đất để tận dụng địa hình và tạo hiệu ứng bất ngờ. Điểm đầu của đường trượt là \(H\left( { - 3;a} \right)\) và điểm cuối là \(K\left( {8;0} \right)\) và ngay dưới điểm \(K\) là một bể bơi. Để tiếp cận đường trượt, một cầu thang cong có dạng parabol \(y = f\left( x \right)\) có đỉnh là điểm \(M\left( { - 8;0} \right)\) được xây dựng, đảm bảo độ dốc vừa phải và an toàn cho người sử dụng.

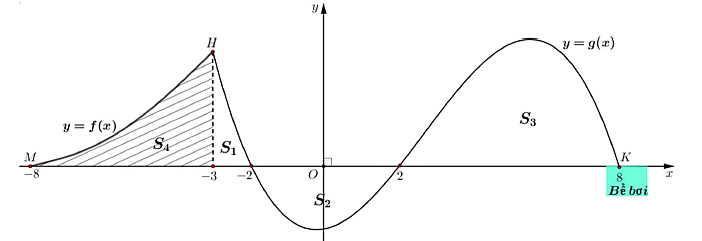
Các diện tích hình phẳng được tạo bởi các đồ thị \(y = f\left( x \right),y = g\left( x \right),x = - 3\) và trục hoành như hình vẽ. Để đảm bảo an toàn tuyệt đối cho người chơi và tính ổn định của công trình, các kỹ sư cần đặc biệt chú trọng đến phần đường trượt nằm dưới lòng đất. Hãy xác định độ cao lớn nhất mà đường trượt chìm xuống so với mặt đất (đơn vị: mét) biết rằng \({S_1} + {S_3} = {S_2} + {S_4} + \frac{{109}}{{12}}\) (làm tròn kết quả đến hàng phần trăm).

Đáp án: \(2,95\).

+ Parabol \(\left( P \right):y = f\left( x \right)\) có đỉnh là điểm \(M\left( { - 8;0} \right)\) nên \(f\left( x \right) = k{\left( {x + 8} \right)^2},\left( {k \ne 0} \right)\).

Ta có \(H\left( { - 3;a} \right) \in \left( P \right)\) nên \(25k = a \Leftrightarrow k = \frac{a}{{25}} \Rightarrow f\left( x \right) = \frac{a}{{25}}{\left( {x + 8} \right)^2}\).

+ Đường cong \(\left( C \right)\):\(y = g\left( x \right)\) là hàm bậc ba có ba nghiệm \(x =  - 2\,;\,x = 2\) và \(x = 8\) nên \(g\left( x \right) = h\left( {{x^2} - 4} \right)\left( {x - 8} \right),\left( {h \ne 0} \right)\).

Ta có \(H\left( { - 3;a} \right) \in \left( C \right)\) nên \( - 55h = a \Leftrightarrow h =  - \frac{a}{{55}}\).

\( \Rightarrow g\left( x \right) =  - \frac{a}{{55}}\left( {{x^2} - 4} \right)\left( {x - 8} \right) =  - \frac{a}{{55}}\left( {{x^3} - 8{x^2} - 4x + 32} \right)\).

+ Dựa vào đồ thị, ta có: \({S_1} = \int\limits_{ - 3}^{ - 2} {g\left( x \right)} \,{\rm{d}}x;\,\,{S_3} = \int\limits_2^8 {g\left( x \right)} \,{\rm{d}}x;\,\,{S_2} =  - \int\limits_{ - 2}^2 {g\left( x \right)} \,{\rm{d}}x;\,\,{S_4} = \int\limits_{ - 8}^{ - 3} {f\left( x \right)} \,{\rm{d}}x\).

\({S_1} + {S_3} = {S_2} + {S_4} + \frac{{109}}{{12}} \Leftrightarrow \int\limits_{ - 3}^{ - 2} {g\left( x \right)} \,{\rm{d}}x + \int\limits_2^8 {g\left( x \right)} \,{\rm{d}}x =  - \int\limits_{ - 2}^2 {g\left( x \right)} \,{\rm{d}}x + \int\limits_{ - 8}^{ - 3} {f\left( x \right)} \,{\rm{d}}x + \frac{{109}}{{12}}\)

\( \Leftrightarrow \int\limits_{ - 3}^{ - 2} {g\left( x \right){\rm{d}}x}  + \int\limits_{ - 2}^2 {g\left( x \right){\rm{d}}x}  + \int\limits_2^8 {g\left( x \right){\rm{d}}x}  = \int\limits_{ - 8}^{ - 3} {f\left( x \right){\rm{d}}x}  + \frac{{109}}{{12}}\)

\( \Leftrightarrow \int\limits_{ - 3}^8 {g\left( x \right){\rm{d}}x}  = \int\limits_{ - 8}^{ - 3} {f\left( x \right){\rm{d}}x}  + \frac{{109}}{{12}}\)

\( \Leftrightarrow \int\limits_{ - 3}^8 { - \frac{a}{{55}}\left( {{x^3} - 8{x^2} - 4x + 32} \right){\rm{d}}x}  = \int\limits_{ - 8}^{ - 3} {\frac{a}{{25}}{{\left( {x + 8} \right)}^2}{\rm{d}}x}  + \frac{{109}}{{12}}\)

\( \Leftrightarrow \frac{{209}}{{60}} \cdot a = \frac{5}{3} \cdot a + \frac{{109}}{{12}} \Leftrightarrow a = 5\).

Suy ra \(g\left( x \right) =  - \frac{1}{{11}}\left( {{x^3} - 8{x^2} - 4x + 32} \right)\); \(g'\left( x \right) =  - \frac{1}{{11}}\left( {3{x^2} - 16x - 4} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{8 + 2\sqrt {19} }}{3}\\x = \frac{{8 - 2\sqrt {19} }}{3}\end{array} \right.\).

Bảng biến thiên

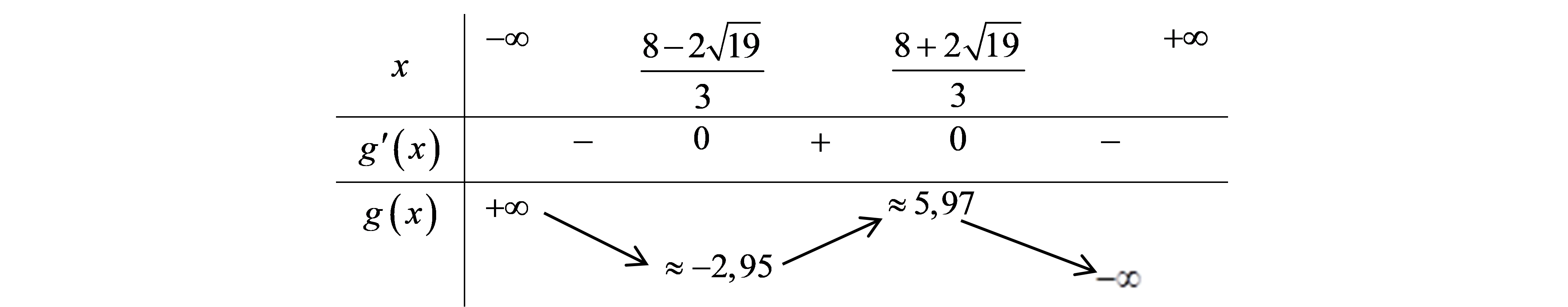
Vậy độ cao lớn nhất mà đường trượt chìm xuống so với mặt đất là xấp xỉ \(2,95\,{\rm{m}}\).